Центральная предельная теорема
Как быстро среднее арифметическое сходится к математическому ожиданию?
Пусть, как в законе больших чисел Чебышева,  - сумма
- сумма  независимых и одинаково распределенных величин с
конечной
дисперсией.
Тогда по ЗБЧ
независимых и одинаково распределенных величин с
конечной
дисперсией.
Тогда по ЗБЧ 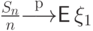 с ростом
с ростом  .
Или, после приведения к общему знаменателю,
.
Или, после приведения к общему знаменателю,

 мы получили в пределе нуль (в смысле
некоторой,
все равно какой, сходимости), резонно задать себе вопрос:
а не слишком ли на большую величину мы поделили? Нельзя ли поделить
на что-нибудь, растущее к бесконечности медленнее, чем
мы получили в пределе нуль (в смысле
некоторой,
все равно какой, сходимости), резонно задать себе вопрос:
а не слишком ли на большую величину мы поделили? Нельзя ли поделить
на что-нибудь, растущее к бесконечности медленнее, чем  ,
чтобы получить в пределе не нуль (но и не бесконечность)?
,
чтобы получить в пределе не нуль (но и не бесконечность)?Можно поставить тот же вопрос иначе. Есть последовательность, стремящаяся к нулю. Можно ли ее домножить на что-либо растущее, чтобы "погасить" это стремление к нулю и получить, тем самым, что-нибудь конечное и ненулевое в пределе?
Оказывается, что уже последовательность случайных величин
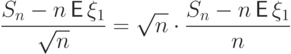
Слабая сходимость
Пусть задана последовательность случайных величин 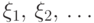 ,
задано некоторое распределение
,
задано некоторое распределение 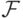 с функцией
распределения
с функцией
распределения 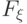 и пусть
и пусть  - произвольная случайная
величина, имеющая распределение
- произвольная случайная
величина, имеющая распределение 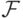 .
.
Определение 46.
Говорят, что последовательность случайных величин 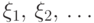 сходится слабо или сходится по распределению
к случайной величине
сходится слабо или сходится по распределению
к случайной величине  и пишут:
и пишут:  ,
если для любого
,
если для любого  такого, что функция распределения
такого, что функция распределения 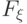 непрерывна
в точке
непрерывна
в точке  , имеет место сходимость
, имеет место сходимость  при
при 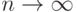 .
.
Итак, слабая сходимость - это сходимость функций распределения во всех точках непрерывности предельной функции распределения.
Замечание.
Заметим, что сходимость  есть сходимость распределений, а не случайных величин:
если "предельную" величину
есть сходимость распределений, а не случайных величин:
если "предельную" величину  заменить на другую величину
заменить на другую величину 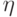 с тем же распределением,
ничего не изменится: в том же смысле
с тем же распределением,
ничего не изменится: в том же смысле  .
.
Следующее свойство очевидно. Если нет - нужно вернуться к определению и свойствам функций распределения.
Свойство 25.
Если  , и функция распределения
, и функция распределения 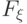 непрерывна в точках
непрерывна в точках  и
и  , то
, то 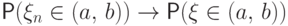 .
Если во всех точках
.
Если во всех точках  и
и  непрерывности
функции распределения
непрерывности
функции распределения 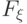 имеет место сходимость
имеет место сходимость 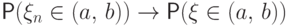 ,
то
,
то  .
.
Вместо открытого интервала 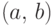 можно взять полуоткрытый
или замкнутый.
можно взять полуоткрытый
или замкнутый.
Свойство 26.
- Если
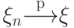 , то
, то  .
. - Если
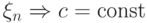 , то
, то 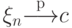 .
.
Итак, сходимость по вероятности влечет слабую сходимость. Обратное утверждение в общем случае смысла не имеет (см. замечание выше). Однако из слабой сходимости к постоянной вытекает сходимость по вероятности.
Доказательство. Первое утверждение мы докажем чуть позже.
Докажем, что слабая сходимость к постояннной влечет
сходимость по вероятности.
Пусть  , т.е.
, т.е.
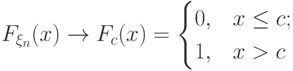
 , являющемся точкой непрерывности предельной функции
, являющемся точкой непрерывности предельной функции 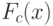 , т.е. при всех
, т.е. при всех  .
.Возьмем произвольное  и докажем,
что
и докажем,
что  :
:
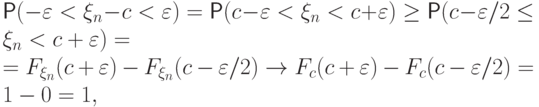
 и
и  функция
функция  непрерывна, и, следовательно, имеет место сходимость
последовательностей
непрерывна, и, следовательно, имеет место сходимость
последовательностей 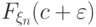 к
к 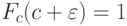 и
и 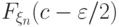 к
к 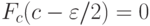 .
.Осталось заметить, что  не бывает больше
не бывает больше  , так что по свойству предела зажатой
последовательности
, так что по свойству предела зажатой
последовательности  .
.
Следующее свойство приводит пример операций, которые можно применять к слабо сходящимся последовательностям - домножать их на последовательности, сходящиеся по вероятности к постоянным величинам.
Замечание
Свойство "предел суммы равен сумме пределов" для слабой сходимости
просто бессмысленно:
сходимости  ,
, 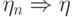 означают, что нам известны предельные распределения этих
последовательностей. Но предельное распределение их суммы
может быть различным в зависимости от совместного распределения
означают, что нам известны предельные распределения этих
последовательностей. Но предельное распределение их суммы
может быть различным в зависимости от совместного распределения 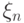 и
и 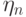 . Иное дело, когда одно из
предельных распределений вырождено. Тогда предельная функция
распределения суммы или произведения определена однозначно.
. Иное дело, когда одно из
предельных распределений вырождено. Тогда предельная функция
распределения суммы или произведения определена однозначно.
