Лекция 14: Характеристические функции
Определение и примеры
В этой лекции 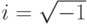 - мнимая единица,
- мнимая единица,  -
вещественная переменная,
-
вещественная переменная, 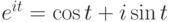 - формула
Эйлера,
- формула
Эйлера,  -
способ вычисления математического ожидания комплекснозначной
случайной величины
-
способ вычисления математического ожидания комплекснозначной
случайной величины 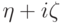 ,
если математические ожидания ее действительной
(
,
если математические ожидания ее действительной
( 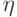 ) и мнимой (
) и мнимой (  ) частей существуют.
) частей существуют.
Как всегда,
модулем комплексного числа  называется
положительное число
называется
положительное число  , так что
, так что 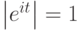 .
.
Определение 47.
Функция  вещественной
переменной
вещественной
переменной  называется
характеристической функцией случайной
величины
называется
характеристической функцией случайной
величины  .
.
Пример 73.
Пусть случайная величина  имеет распределение Бернулли с
параметром
имеет распределение Бернулли с
параметром 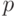 .
Ее характеристическая функция равна
.
Ее характеристическая функция равна
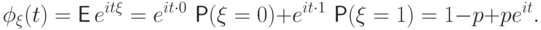
Пример 74.
Пусть случайная величина  имеет биномиальное распределение
с параметрами
имеет биномиальное распределение
с параметрами 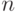 и
и 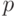 .
Ее характеристическая функция равна
.
Ее характеристическая функция равна
Пример 75.
Пусть случайная величина  имеет распределение Пуассона с
параметром
имеет распределение Пуассона с
параметром 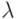 .
Ее характеристическая функция равна
.
Ее характеристическая функция равна

Пример 76.
Пусть случайная величина  имеет гамма-распределение с
параметрами
имеет гамма-распределение с
параметрами  и
и 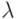 .
Ее характеристическая функция равна
.
Ее характеристическая функция равна
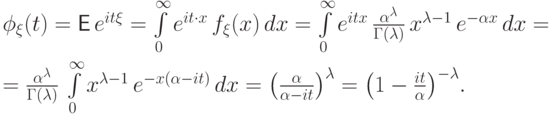
 дает
дает
В качестве следствия получим, что для случайной величины  с
показательным распределением
с
показательным распределением 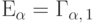 характеристическая функция
равна
характеристическая функция
равна  .
.
Пример 77.
Пусть случайная величина  имеет стандартное
нормальное
распределение. Ее характеристическая функция равна
имеет стандартное
нормальное
распределение. Ее характеристическая функция равна
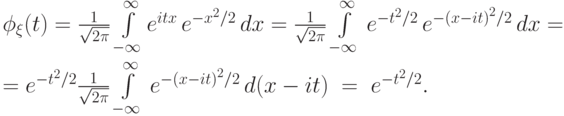
При интегрировании мы выделили полный квадрат в показателе
экспоненты и вспомнили, что интеграл по  от функции
от функции 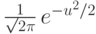 равен
единице.
равен
единице.
Свойства характеристических функций
(Ф1). Характеристическая функция всегда существует:
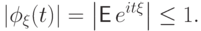
Полезно вспомнить, что даже  существует не всегда.
существует не всегда.
Доказательство. Воспользуемся свойством  , равносильным
неравенству
, равносильным
неравенству  :
:
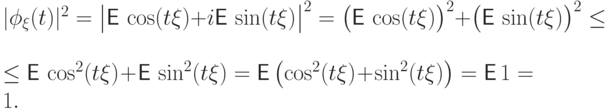
(Ф2). По характеристической функции однозначно восстанавливается распределение (функция распределения, плотность или таблица распределения). Другими словами, если две случайные величины имеют одинаковые характеристические функции, то и распределения этих величин совпадают.
Формулы, с помощью которых по характеристической функции восстанавливается распределение, в анализе называют формулами "обратного преобразования Фурье". Например, если модуль характеристической функции интегрируем на всей прямой, то у случайной величины есть плотность распределения и она находится по формуле

(Ф3).
Характеристическая функция случайной величины  связана с характеристической функцией случайной величины
связана с характеристической функцией случайной величины  равенством
равенством

