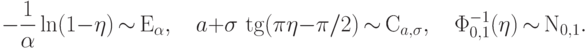Преобразования случайных величин
Измеримость функций от случайных величин
Пусть на вероятностном пространстве 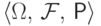 задана случайная величина
задана случайная величина  . Если
. Если 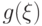 -
случайная величина, то полезно уметь находить распределение
-
случайная величина, то полезно уметь находить распределение 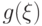 по распределению
по распределению  . Эта проблема возникает,
например,
при моделировании случайных величин с заданным распределением. Датчик случайных
чисел может генерировать лишь значения случайных величин с равномерным
распределением. Если же нам необходимы значения показательно распределенной
случайной величины, нужно найти преобразование,
которое из равномерного распределения сделает показательное.
. Эта проблема возникает,
например,
при моделировании случайных величин с заданным распределением. Датчик случайных
чисел может генерировать лишь значения случайных величин с равномерным
распределением. Если же нам необходимы значения показательно распределенной
случайной величины, нужно найти преобразование,
которое из равномерного распределения сделает показательное.
Вопрос об измеримости 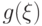 решает следующая теорема.
решает следующая теорема.
Теорема 26.
Пусть  - случайная величина, а
- случайная величина, а 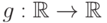 -
борелевская (измеримая по Борелю) функция, т.е. такая, что для всякого
борелевского множества
-
борелевская (измеримая по Борелю) функция, т.е. такая, что для всякого
борелевского множества 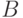 его прообраз
его прообраз 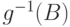 есть
снова борелевское
множество.
Тогда
есть
снова борелевское
множество.
Тогда 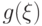 - случайная величина.
- случайная величина.
Доказательство.
Проверим, что прообраз любого борелевского множества
при отображении  является событием.
Возьмем произвольное
является событием.
Возьмем произвольное 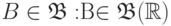 и положим
и положим 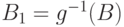 . Множество
. Множество 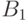 борелевское, так как функция
борелевское, так как функция 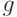 измерима по Борелю. Но тогда
измерима по Борелю. Но тогда 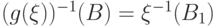 . Это множество принадлежит
. Это множество принадлежит 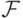 ,
поскольку
,
поскольку 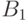 - борелевское множество и
- борелевское множество и  -
случайная величина.
-
случайная величина.
Борелевскими являются все привычные нам функции. Функцией, неизмеримой по Борелю, будет, например, индикаторная функция неизмеримого множества Витали. Вообще говоря, неизмеримые функции суть объекты экзотические, в обычной жизни не встречающиеся.
Заметим, что совершенно аналогично решается вопрос об измеримости
функции от нескольких случайных величин, если он принимает значения
в  или в
или в 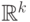 .
.
Распределения функций от случайных величин
Линейные и монотонные преобразования.
Если  имеет дискретное распределение, то любая функция
имеет дискретное распределение, то любая функция 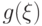 от нее также имеет дискретное распределение,
и таблица распределения
от нее также имеет дискретное распределение,
и таблица распределения 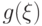 находится просто по определению.
Поэтому мы будем рассматривать преобразования случайных величин
с абсолютно непрерывными распределениями.
находится просто по определению.
Поэтому мы будем рассматривать преобразования случайных величин
с абсолютно непрерывными распределениями.
Пусть случайная величина  имеет функцию распределения
имеет функцию распределения 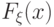 и плотность
распределения
и плотность
распределения 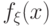 . Построим с помощью борелевской
функции
. Построим с помощью борелевской
функции 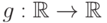 случайную величину
случайную величину 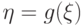 .
Требуется найти плотность распределения величины
.
Требуется найти плотность распределения величины 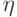 (если
таковая существует).
(если
таковая существует).
Замечание.
Плотность распределения случайной величины 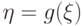 существует далеко не при любых функциях
существует далеко не при любых функциях 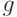 .
Так, если функция
.
Так, если функция 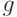 кусочно-постоянна, то
кусочно-постоянна, то 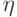 имеет
дискретное распределение.
имеет
дискретное распределение.
Для отыскания плотности распределения мы не можем просто
продифференцировать функцию распределения,
поскольку не знаем, существует ли плотность.
Следует доказать, что распределение абсолютно непрерывно.
Но доказывая это, мы попутно найдем и плотность распределения.
Действительно, у нас есть следующий путь доказательства
абсолютной непрерывности распределения.
Если
для любого 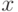 мы представим функцию распределения величины
мы представим функцию распределения величины 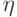 в виде
в виде
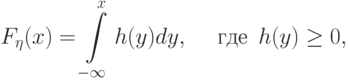
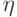 можно взять
подынтегральную функцию:
можно взять
подынтегральную функцию: 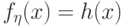 .
Другой путь -
продифференцировать функцию распределения и убедиться, что производная
является плотностью распределения, т.е. обладает необходимыми для плотности
свойствами.
.
Другой путь -
продифференцировать функцию распределения и убедиться, что производная
является плотностью распределения, т.е. обладает необходимыми для плотности
свойствами.Теорема 27.
Пусть  имеет функцию распределения
имеет функцию распределения 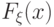 и плотность
распределения
и плотность
распределения 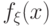 , и постоянная
, и постоянная 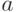 отлична от
нуля.
Тогда случайная величина
отлична от
нуля.
Тогда случайная величина  имеет плотность
распределения
имеет плотность
распределения
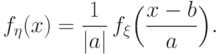
Доказательство.
Пусть сначала 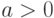 .
.
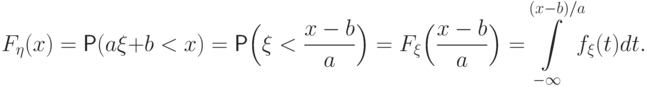
 заменим на
новую переменную
заменим на
новую переменную  так:
так: 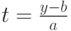 . Тогда
. Тогда  ,
нижняя граница области интегрирования
,
нижняя граница области интегрирования  перейдет в
перейдет в 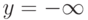 , верхняя граница
, верхняя граница 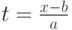 перейдет в
перейдет в 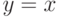 .
Получим
.
Получим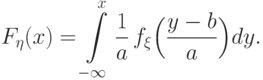
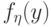 случайной величины
случайной величины  при
при 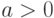 .
.Пусть теперь 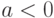 .
.
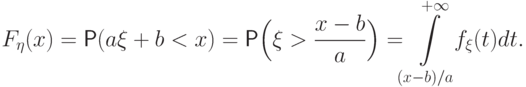
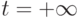 перейдет
в
перейдет
в 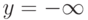 ,
поскольку
,
поскольку 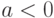 . Получим
. Получим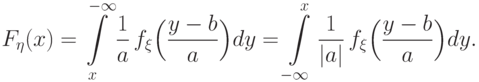
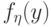 случайной величины
случайной величины  при
при 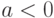 .
.Из теоремы 27 следуют уже знакомые нам утверждения.
Следствие 4.
Если  , то
, то 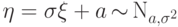 .
.
Доказательство. Действительно,
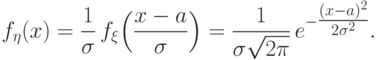
Следствие 5.
Если  , то
, то  .
.
Следствие 6.
Если 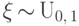 , то
, то 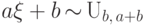 при
при 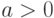 .
.
Следствие 7.
Если 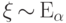 , то
, то 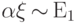 .
.
Квантильное преобразование. Полезно уметь строить случайные величины с заданным распределением по равномерно распределенной случайной величине (например, по результату датчика случайных чисел).
Теорема 28.
Пусть функция распределения 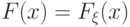 непрерывна. Тогда
случайная
величина
непрерывна. Тогда
случайная
величина 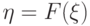 имеет равномерное на отрезке
имеет равномерное на отрезке ![[0,\,1]](/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png) распределение.
распределение.
Доказательство.
Найдем функцию распределения случайной величины 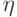 .
Заметим, что всегда
.
Заметим, что всегда 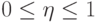 . Предположим сначала, что
функция
. Предположим сначала, что
функция 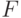 всюду возрастает. Тогда она обратима, и поэтому
всюду возрастает. Тогда она обратима, и поэтому
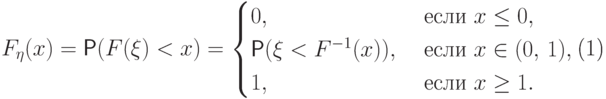 |
( 16) |
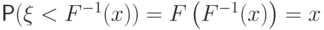 ,
т.е.
,
т.е. 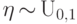 .
.Если функция 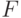 не является всюду возрастающей, то у нее есть
участки постоянства.
В этом случае просто обозначим через
не является всюду возрастающей, то у нее есть
участки постоянства.
В этом случае просто обозначим через 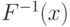 самую левую точку
из замкнутого множества
самую левую точку
из замкнутого множества  . При таком понимании "обратной"
функции равенства (16) остаются
справедливыми вместе с равенством
. При таком понимании "обратной"
функции равенства (16) остаются
справедливыми вместе с равенством 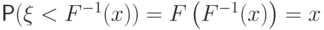 для любого
для любого  .
.
Обратим теорему 28. Следующее
утверждение верно не только
для непрерывных, но для любых функций распределения 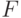 .
Обозначим через
.
Обозначим через 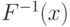 точную нижнюю грань множества тех
точную нижнюю грань множества тех  , для которых
, для которых 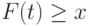 :
:
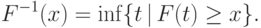
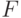 это определение "обратной
функции" совпадает с введенным в доказательстве
теоремы 28.
это определение "обратной
функции" совпадает с введенным в доказательстве
теоремы 28.Теорема 29.
Пусть 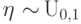 , а
, а 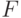 -
произвольная
функция распределения. Тогда случайная
величина
-
произвольная
функция распределения. Тогда случайная
величина 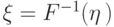 "квантильное
преобразование"
над
"квантильное
преобразование"
над 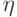 имеет функцию распределения
имеет функцию распределения 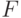 .
.
Следствие 8.
Пусть 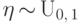 . Верны соотношения:
. Верны соотношения: