Условная вероятность и независимость
Условная вероятность
Пример 29. Игральная кость подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало нечетное число очков?
Пусть событие 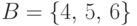 означает, что выпало более трех
очков,
событие
означает, что выпало более трех
очков,
событие 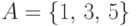 - выпало нечетное число очков. Как
понимать вероятность события
- выпало нечетное число очков. Как
понимать вероятность события  , если известно, что
, если известно, что  случилось?
Знаем, что произошло событие
случилось?
Знаем, что произошло событие  , но все равно не знаем,
что именно выпало на кости. Однако теперь возможностей осталось только
три:
могло выпасть
, но все равно не знаем,
что именно выпало на кости. Однако теперь возможностей осталось только
три:
могло выпасть 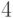 ,
, 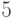 или
или  очков.
Событию
очков.
Событию  из этих равновозможных исходов благоприятен
единственный исход:
выпадение пяти очков.
Поэтому искомая вероятность равна
из этих равновозможных исходов благоприятен
единственный исход:
выпадение пяти очков.
Поэтому искомая вероятность равна 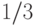 .
.
Итак, при вычислении условной вероятности события  при
случившемся событии
при
случившемся событии  мы ищем
долю исходов, благоприятствующих
мы ищем
долю исходов, благоприятствующих  , среди всех исходов
события
, среди всех исходов
события  .
Эту условную вероятность будем обозначать
.
Эту условную вероятность будем обозначать 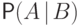 .
.
Определение 12.
Условной вероятностью события  при условии, что произошло
событие
при условии, что произошло
событие  , называется число
, называется число
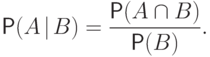
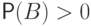 .
.Следует отличать условную вероятность одного события при осуществлении другого от вероятности им одновременно произойти.
Это определение бывает полезно использовать не для вычисления условной вероятности, а для последовательного вычисления вероятности нескольким событиям случиться одновременно, если известны соответствующие условные вероятности. Справедливы следующие "теоремы умножения вероятностей".
Теорема 9.
Если 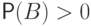 и
и 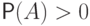 , то
, то

Теорема 10. Для любых событий  верно равенство:
верно равенство:

Упражнение. Доказать теорему 10
методом математической индукции.
Доказать, что все условные вероятности в теореме 10 определены тогда и только тогда, когда 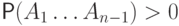 .
.
Независимость событий
Определение 13.
События  и
и  называются
независимыми,
если
называются
независимыми,
если  .
.
Пример 30. Из колоды в 36 карт наугад берут одну. Независимы ли события "вынут туз" и "вынута пиковая карта"?
Решение.
Вероятность вытянуть туза равна 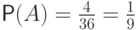 .
Вероятность вытянуть пиковую карту равна
.
Вероятность вытянуть пиковую карту равна 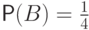 .
Пересечение этих событий означает появление туза пик и имеет вероятность
.
Пересечение этих событий означает появление туза пик и имеет вероятность 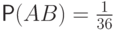 .
Cобытия
.
Cобытия  и
и  независимы, так как
независимы, так как 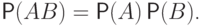
Естественно считать события  и
и  независимыми,
когда условная вероятность
независимыми,
когда условная вероятность  при условии, что
при условии, что  произошло, остается такой же,
как и безусловная.
Убедимся, что этим свойством обладают события, независимые согласно определению
13.
произошло, остается такой же,
как и безусловная.
Убедимся, что этим свойством обладают события, независимые согласно определению
13.
Свойство 4.
Пусть 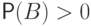 . Тогда события
. Тогда события  и
и  независимы
тогда и только тогда, когда
независимы
тогда и только тогда, когда  .
.
Упражнение. Доказать по определению условной вероятности.
Независимые события возникают, например, при повторении испытаний. Выпадение герба и выпадение решки при двух разных бросках монеты независимы. Любые события, относящиеся к двум разным подбрасываниям игральной кости, независимы.
Свойство 5.
Пусть события  и
и  несовместны.
Тогда независимыми они будут только в том случае, если
несовместны.
Тогда независимыми они будут только в том случае, если 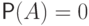 или
или 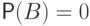 .
.
Это свойство означает, что в невырожденном случае (когда вероятности событий
положительны) несовместные события не могут
быть независимыми. Зависимость между ними - просто причинно следственная:
если 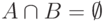 , то
, то 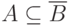 ,
т.е. при выполнении
,
т.е. при выполнении  событие
событие  не происходит.
не происходит.
Упражнение. Доказать с помощью свойства монотонности вероятности, что
событие  ,
вероятность которого равна нулю или единице,
не зависит ни от какого события
,
вероятность которого равна нулю или единице,
не зависит ни от какого события  , в том числе и от самого себя.
, в том числе и от самого себя.
Свойство 6.
Если события  и
и  независимы, то независимы
и события
независимы, то независимы
и события  и
и  ,
,  и
и  ,
,  и
и  .
.
Доказательство.
Так как 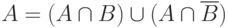 , и события
, и события 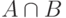 и
и 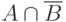 несовместны,
то
несовместны,
то 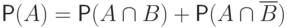 .
Поэтому
.
Поэтому 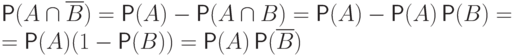 .
Остальные утверждения вытекают из первого.
.
Остальные утверждения вытекают из первого.
Если у нас не два, а большее число событий, выполнение только одного
равенства  вовсе не означает независимости этих событий. Например, при таком равенстве
события
вовсе не означает независимости этих событий. Например, при таком равенстве
события 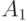 и
и 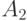 вполне могут оказаться зависимыми.
вполне могут оказаться зависимыми.
Пример 31.
Пусть 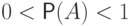 . События
. События 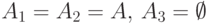 обладают свойством
обладают свойством
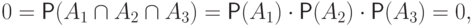
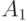 и
и 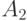 быть зависимыми:
быть зависимыми: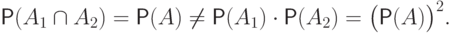
Хотелось бы независимостью нескольких событий считать такое свойство, при
котором
любые комбинации этих событий будут независимы между собой: например,
независимы  и
и 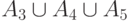 .
.
Определение 14.
События  называются
независимыми в совокупности, если для любого
называются
независимыми в совокупности, если для любого 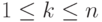 и
любого
набора различных меж собой индексов
и
любого
набора различных меж собой индексов  имеет место равенство
имеет место равенство
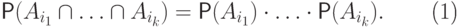 |
( 4.1) |
Замечание.
Если события  независимы в совокупности, то
они попарно независимы, т.е. любые два
события
независимы в совокупности, то
они попарно независимы, т.е. любые два
события  и
и 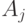 независимы. Достаточно в равенстве (4.1)
взять
независимы. Достаточно в равенстве (4.1)
взять  . Обратное, как показывает следующий пример, неверно: из
попарной независимости
не вытекает независимость в совокупности.
. Обратное, как показывает следующий пример, неверно: из
попарной независимости
не вытекает независимость в совокупности.
Пример 32(пример Бернштейна).
Рассмотрим правильный тетраэдр, три грани которого окрашены соответственно
в красный, синий, зеленый цвета, а четвертая грань содержит все три цвета.
Событие  (
(  ,
,  ) означает, что выпала
грань, содержащая
красный (соответственно синий, зеленый) цвета.
) означает, что выпала
грань, содержащая
красный (соответственно синий, зеленый) цвета.
Вероятность каждого из этих событий равна  , так как каждый цвет
есть на двух гранях из четырех. Вероятность пересечения
любых двух событий равна
, так как каждый цвет
есть на двух гранях из четырех. Вероятность пересечения
любых двух событий равна  ,
так как только одна грань из четырех содержит два цвета.
Поэтому любые два события из трех независимы, так как
,
так как только одна грань из четырех содержит два цвета.
Поэтому любые два события из трех независимы, так как 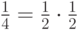 .
.
Но вероятность события 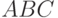 (на грани есть все три цвета) тоже
равна
(на грани есть все три цвета) тоже
равна  ,
а не
,
а не  ,
т.е. события не являются независимыми в совокупности.
,
т.е. события не являются независимыми в совокупности.

 .
.