Центральная предельная теорема
Центральная предельная теорема
Мы будем называть следующее утверждение "ЦПТ Ляпунова",
но сформулируем и докажем
теорему Ляпунова только в частном
случае - для последовательности
независимых и одинаково распределенных случайных величин.
Как и ранее, через 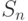 обозначена сумма первых
обозначена сумма первых  случайных величин в последовательности:
случайных величин в последовательности:  .
.
Теорема 40 (ЦПТ Ляпунова).
Пусть 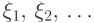 - независимые и одинаково
распределенные
случайные величины с конечной и ненулевой дисперсией:
- независимые и одинаково
распределенные
случайные величины с конечной и ненулевой дисперсией: 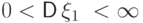 .
Тогда имеет место слабая сходимость
.
Тогда имеет место слабая сходимость
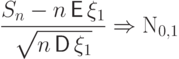
Пользуясь определением и свойствами слабой сходимости
и заметив, что функция распределения  любого нормального закона непрерывна всюду на
любого нормального закона непрерывна всюду на  ( почему?),
утверждение ЦПТ можно сформулировать любым из следующих способов.
( почему?),
утверждение ЦПТ можно сформулировать любым из следующих способов.
Следствие 18.
Пусть 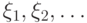 - независимые и одинаково
распределенные
случайные величины с конечной и ненулевой дисперсией.
Тогда выполнены утверждения:
- независимые и одинаково
распределенные
случайные величины с конечной и ненулевой дисперсией.
Тогда выполнены утверждения:
- для любых вещественных
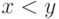 при
при 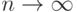 имеет место сходимость
имеет место сходимость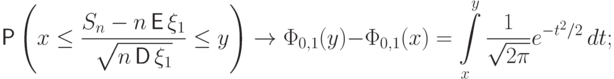
- если
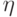 - произвольная случайная величина
со стандартным нормальным
распределением, то
- произвольная случайная величина
со стандартным нормальным
распределением, то
Мы докажем центральную предельную теорему и закон больших чисел в форме Хинчина в следующей лекции. Нам потребуется для этого познакомиться с мощным математическим инструментом, который в математике обычно называют преобразованиями Фурье, а в теории вероятностей - характеристическими функциями.
Получим в качестве следствия из ЦПТ Ляпунова предельную теорему Муавра и Лапласа. Подобно ЗБЧ Бернулли, это утверждение годится только для схемы Бернулли.
Теорема 41 (предельная теорема Муавра - Лапласа).
Пусть событие  может произойти в любом из
может произойти в любом из  независимых испытаний
с одной и той же вероятностью
независимых испытаний
с одной и той же вероятностью  и пусть
и пусть 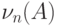 - число осуществлений
события
- число осуществлений
события  в
в  испытаниях.
Тогда
испытаниях.
Тогда
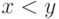 имеет место сходимость
имеет место сходимость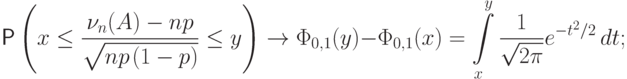
Доказательство.
Величина 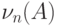 есть сумма независимых,
одинаково распределенных случайных величин, имеющих распределение Бернулли
с параметром, равным вероятности успеха
есть сумма независимых,
одинаково распределенных случайных величин, имеющих распределение Бернулли
с параметром, равным вероятности успеха  :
: 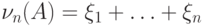 , где
, где 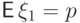 ,
, 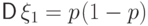 .
Осталось воспользоваться ЦПТ.
.
Осталось воспользоваться ЦПТ.
