Многомерные распределения
Примеры многомерных распределений
Приведем два наиболее употребительных примера абсолютно непрерывных многомерных распределений.
Равномерное распределение.
Пусть  - борелевское множество с конечной
лебеговой
мерой
- борелевское множество с конечной
лебеговой
мерой  . Говорят, что вектор
. Говорят, что вектор 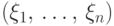 имеет
равномерное распределение в области
имеет
равномерное распределение в области  ,
если плотность совместного распределения
,
если плотность совместного распределения 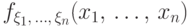 постоянна в области
постоянна в области  и равна нулю вне этой области:
и равна нулю вне этой области:
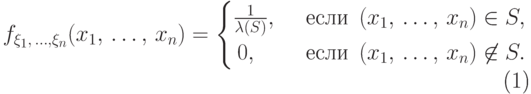 |
( 15) |
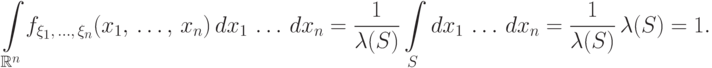
Как и в одномерном случае, вектор 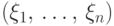 с
равномерным
распределением в области
с
равномерным
распределением в области  есть просто вектор координат точки,
брошенной
наудачу в область
есть просто вектор координат точки,
брошенной
наудачу в область  .
.
Многомерное нормальное
распределение.
Пусть  - положительно определенная симметричная
матрица
- положительно определенная симметричная
матрица  , матрица
, матрица 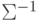 -
обратная к
-
обратная к  , и
, и 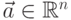 -
-  -мерный вектор-столбец. Транспонированный
вектор мы будем обозначать так:
-мерный вектор-столбец. Транспонированный
вектор мы будем обозначать так: 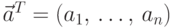 .
.
Говорят, что вектор 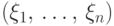 имеет
многомерное нормальное распределение
имеет
многомерное нормальное распределение 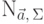 с вектором средних
с вектором средних 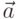 и матрицей ковариаций
и матрицей ковариаций  ,
если плотность совместного распределения
,
если плотность совместного распределения 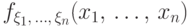 равна
равна
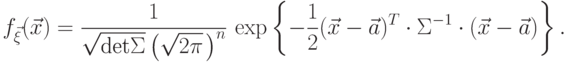
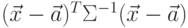 в показателе
экспоненты является квадратичной формой от переменных
в показателе
экспоненты является квадратичной формой от переменных  .
Действительно, для матрицы
.
Действительно, для матрицы 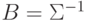 с элементами
с элементами 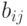 имеем
имеем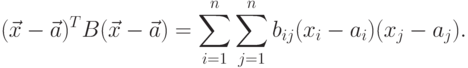
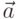 и матрицей ковариаций
и матрицей ковариаций  ".
".В частном случае, когда  - диагональная матрица
с элементами
- диагональная матрица
с элементами  на диагонали,
совместная
плотность превращается в произведение плотностей нормальных случайных
величин:
на диагонали,
совместная
плотность превращается в произведение плотностей нормальных случайных
величин:
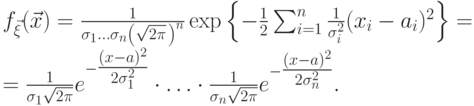
 .
.Роль совместного распределения
Если нам известно совместное распределение двух или нескольких случайных величин, становится возможным отыскать распределение суммы, разности, произведения, частного, иных функций от этих случайных величин. Заметим (но не будем доказывать), что применение к набору случайных величин многих привычных нам функций не выводит нас из класса случайных величин. Интересующийся читатель может попробовать доказать, например, что сумма двух случайных величин есть снова случайная величина.
Следующие два примера показывают, что знания только частных распределений двух случайных величин недостаточно для отыскания распределения, например, суммы этих величин. Для этого необходимо знать их совместное распределение. Распределение суммы (и любой иной функции) не определяется, вообще говоря, распределениями слагаемых: при одних и тех же распределениях слагаемых распределение суммы может быть разным в зависимости от совместного} распределения слагаемых.
Пример 42.
Рассмотрим две случайные величины  и
и 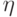 с одним
и тем же
распределением Бернулли с параметром
с одним
и тем же
распределением Бернулли с параметром 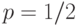 и следующей таблицей
совместного
распределения: для
и следующей таблицей
совместного
распределения: для  положим
положим
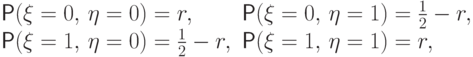
Если  , то
, то 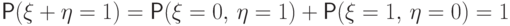 ,
т.е. распределение
,
т.е. распределение  вырождено в точке
вырождено в точке  .
.
Если 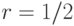 , то
, то 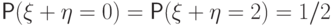 ,
т.е.
,
т.е.  имеет
невырожденное дискретное
распределение, принимая значения
имеет
невырожденное дискретное
распределение, принимая значения  и
и  с равными
вероятностями.
с равными
вероятностями.
Взяв 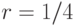 , получим
, получим  ,
, 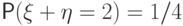 и
и 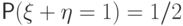 , т.е.
, т.е. 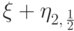 .
.
Если взять 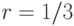 , получим
, получим  ,
, 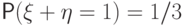 и
и  , т.е.
, т.е.  принимает
значения
принимает
значения 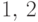 и
и  с равными вероятностями (это не биномиальное распределение).
с равными вероятностями (это не биномиальное распределение).
Еще раз отметим, что частные распределения  и
и 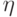 от
от  не зависят. Распределение
суммы меняется вместе с совместным распределением
не зависят. Распределение
суммы меняется вместе с совместным распределением  и
и 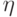 при неизменных частных распределениях величин
при неизменных частных распределениях величин  и
и 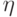 .
.
Пример 43.
Пусть случайная величина  имеет стандартное нормальное
распределение.
имеет стандартное нормальное
распределение.
Возьмем  .
Тогда
.
Тогда 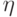 тоже имеет стандартное нормальное распределение, а
сумма
тоже имеет стандартное нормальное распределение, а
сумма 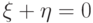 имеет вырожденное распределение.
имеет вырожденное распределение.
Возьмем теперь  .
Тогда сумма
.
Тогда сумма  имеет уже не вырожденное, а нормальное
распределение
имеет уже не вырожденное, а нормальное
распределение  ( проверить ).
( проверить ).
Распределение функции нескольких случайных величин может определяться их частными распределениями только если совместное распределение этих случайных величин определяется их частными распределениями. Так бывает для независимых случайных величин.
