Случайные величины и их распределения
Свойства абсолютно непрерывного распределения.
Пусть случайная величина  имеет абсолютно непрерывное
распределение
с плотностью
имеет абсолютно непрерывное
распределение
с плотностью 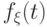 . Тогда функция распределения в любой точке
. Тогда функция распределения в любой точке  может быть найдена по плотности распределения так:
может быть найдена по плотности распределения так:
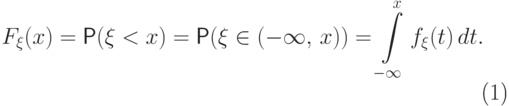 |
( 6.3) |
Свойство 11.
Если случайная величина  имеет абсолютно непрерывное
распределение, то ее функция распределения всюду непрерывна.
имеет абсолютно непрерывное
распределение, то ее функция распределения всюду непрерывна.
Доказательство. Этот факт следует из свойств 7 и 8. Заметим, что оно есть также следствие представления (6.3) и непрерывности интеграла как функции верхнего предела.
Свойство 12.
Если  имеет абсолютно непрерывное
распределение, то ее функция распределения дифференцируема почти всюду,
имеет абсолютно непрерывное
распределение, то ее функция распределения дифференцируема почти всюду,

Замечание.
Термин для "почти всех" означает "для всех, кроме (возможно)  из
некоторого множества нулевой меры Лебега".
из
некоторого множества нулевой меры Лебега".
Заметим, что любая функция распределения дифференцируема почти всюду. Но не у каждого распределения существует плотность распределения. Поэтому возможность дифференцировать функцию распределения никакого отношения к существованию плотности не имеет. Даже если мы дополнительно потребуем непрерывности функции распределения, этого не будет достаточно для абсолютной непрерывности распределения. Например, далее мы увидим, что функция распределения сингулярного распределения непрерывна и дифференцируема почти всюду, однако плотности у этого распределения нет, так как производная функции распределения почти всюду равна нулю.
Опираясь на свойство 12 и формулу
(6.3), можно сформулировать такой критерий
абсолютной непрерывности распределения: распределение с функцией распределения 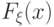 абсолютно непрерывно, если при всех
абсолютно непрерывно, если при всех 
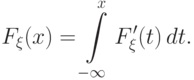
Наконец, очевидным следствием определения абсолютно непрерывного распределения и свойства 11 является следующее свойство.
Свойство 13.
Если случайная величина  имеет абсолютно непрерывное
распределение, то для любых
имеет абсолютно непрерывное
распределение, то для любых  имеют место равенства:
имеют место равенства:
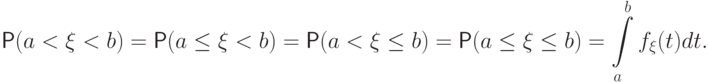
Функция распределения сингулярного распределения.
Для полноты картины посмотрим, какие свойства имеет функция распределения
сингулярного распределения. По определению 25,
случайная величина  с сингулярным распределением принимает
с единичной вероятностью лишь значения из некоторого
борелевского множества
с сингулярным распределением принимает
с единичной вероятностью лишь значения из некоторого
борелевского множества  с нулевой лебеговой мерой.
Поэтому
с нулевой лебеговой мерой.
Поэтому  .
Но по свойству (9), если
.
Но по свойству (9), если 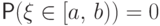 , то
, то  . Это означает, что расти функция распределения
может лишь в точках множества
. Это означает, что расти функция распределения
может лишь в точках множества  . На всем остальном множестве
. На всем остальном множестве  функция распределения имеет почти всюду нулевую
производную.
Тем не менее,
функция распределения имеет почти всюду нулевую
производную.
Тем не менее, 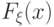 всюду непрерывна, поскольку
всюду непрерывна, поскольку 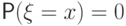 для любой точки
для любой точки 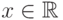 .
Примером такой функции распределения служит лестница Кантора
(
рис.
6.2).
.
Примером такой функции распределения служит лестница Кантора
(
рис.
6.2).
Функция распределения смешанного распределения. Функция распределения смешанного распределения есть выпуклая линейная комбинация функций распределения дискретного, абсолютно непрерывного и сингулярного распределений и наследует типичные черты всех этих распределений. Если смешивать дискретное и абсолютно непрерывное распределения, то функция распределения будет иметь скачки в точках значений дискретного распределения и участки непрерывного роста, приращение на которых восстанавливается по ее производной.

