Случайные величины и их распределения
Функция распределения
Описание распределения набором вероятностей  не
очень удобно: слишком много
существует борелевских множеств. Мы описали дискретные распределения таблицей
распределения, абсолютно непрерывные - плотностью распределения.
Попробуем поискать какой-нибудь универсальный
способ описать любое возможное распределение.
не
очень удобно: слишком много
существует борелевских множеств. Мы описали дискретные распределения таблицей
распределения, абсолютно непрерывные - плотностью распределения.
Попробуем поискать какой-нибудь универсальный
способ описать любое возможное распределение.
Можно поставить вопрос иначе: распределение есть набор вероятностей
попадания в любые борелевские множества на прямой.
Нельзя ли обойтись знанием вероятностей попадания в какой-нибудь
меньший набор множеств на прямой? Борелевская  -алгебра
-алгебра 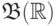 порождается интервалами (равно как и лучами
порождается интервалами (равно как и лучами 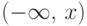 ),
поэтому можно ограничиться
только вероятностями попадания в такие лучи для всех
),
поэтому можно ограничиться
только вероятностями попадания в такие лучи для всех 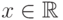 .
А уже с их помощью можно будет определить и вероятность попасть в любое
борелевское множество.
.
А уже с их помощью можно будет определить и вероятность попасть в любое
борелевское множество.
Замечание.
Можно с таким же успехом ограничиться набором вероятностей попадания
в интервалы ![(-\infty,\,x]](/sites/default/files/tex_cache/6ee152d00b378c10e5732a8731f8eb1e.png) , или в
, или в 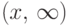 , или
в
, или
в 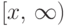 .
.
Определение 27.
Функцией распределения
случайной величины  называется функция
называется функция ![F_\xi: \mathbb R\to [0,\,1]](/sites/default/files/tex_cache/3dbdc35addc93b409fdff1f419373891.png) , при каждом
, при каждом 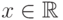 равная
вероятности
случайной величине
равная
вероятности
случайной величине  принимать значения, меньшие
принимать значения, меньшие  :
:

Общие свойства функций распределения.
Теорема 21. Любая функция распределения обладает свойствами:
(F1)
она не убывает:
если 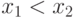 , то
, то 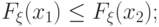
(F2) cуществуют пределы  и
и 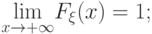
(F3) она в любой точке непрерывна слева
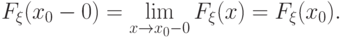
Доказательство свойства (F1)
Для любых чисел 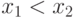 событие
событие 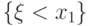 влечет
событие
влечет
событие 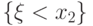 , т.е.
, т.е. 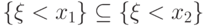 .
Но вероятность - монотонная функция событий, поэтому
.
Но вероятность - монотонная функция событий, поэтому

Для доказательства остальных свойств нам понадобится свойство непрерывности вероятностной меры (теорема 7).
Доказательство свойства (F2).
Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из
монотонности
и ограниченности функции 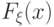 . Остается лишь доказать
равенства
. Остается лишь доказать
равенства 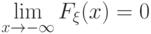 ,
, 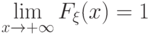 и
и 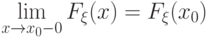 .
Для этого в каждом случае достаточно найти предел по какой-нибудь
подпоследовательности
.
Для этого в каждом случае достаточно найти предел по какой-нибудь
подпоследовательности 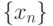 , так как существование предела
влечет совпадение всех частичных пределов.
, так как существование предела
влечет совпадение всех частичных пределов.
Докажем, что  при
при 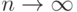 .
Рассмотрим вложенную убывающую последовательность событий
.
Рассмотрим вложенную убывающую последовательность событий 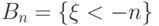 :
:

 всех этих событий состоит из тех и только тех
всех этих событий состоит из тех и только тех  , для которых
, для которых  меньше любого вещественного
числа. Но для любого элементарного исхода
меньше любого вещественного
числа. Но для любого элементарного исхода  значение
значение  вещественно, и не может быть меньше всех вещественных
чисел.
Иначе говоря, пересечение событий
вещественно, и не может быть меньше всех вещественных
чисел.
Иначе говоря, пересечение событий 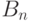 не содержит элементарных
исходов, т.е.
не содержит элементарных
исходов, т.е.  .
По свойству непрерывности меры,
.
По свойству непрерывности меры, 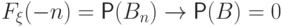 при
при 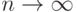 .
.Точно так же докажем остальные свойства.
Покажем, что 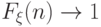 при
при 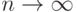 , т.е.
, т.е. 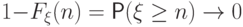 .
Обозначим через
.
Обозначим через 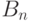 событие
событие 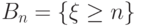 .
События
.
События 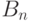 вложены:
вложены:

 этих событий снова пусто: оно означает, что
этих событий снова пусто: оно означает, что  больше
любого вещественного числа.
По свойству непрерывности меры,
больше
любого вещественного числа.
По свойству непрерывности меры,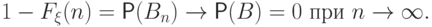
Доказательство свойства (F3).
Достаточно доказать, что 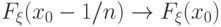 при
при 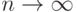 .
Иначе говоря, доказать сходимость к нулю следующей разности:
.
Иначе говоря, доказать сходимость к нулю следующей разности:
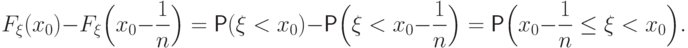
Осталось обозначить событие 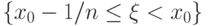 через
через 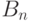 и снова воспользоваться свойством непрерывности меры.
и снова воспользоваться свойством непрерывности меры.
Следующая теорема говорит о том, что три доказанных свойства полностью описывают класс функций распределения. То, что любая функция распределения ими обладает, мы с вами доказали, а теорема утверждает, что любая функция с такими свойствами есть функция распределения.
Теорема 22.
Если функция ![F:\mathbb R\to[0,1]](/sites/default/files/tex_cache/ea54214ae38cee56cdb31830ec730c73.png) удовлетворяет свойствам
(F1)-(F3) ,
то
удовлетворяет свойствам
(F1)-(F3) ,
то  есть функция распределения некоторой случайной величины
есть функция распределения некоторой случайной величины  ,
т.е. найдется вероятностное пространство
,
т.е. найдется вероятностное пространство 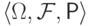 и случайная величина
и случайная величина  на нем такая,
что
на нем такая,
что  .
.
Помимо отмеченных в теореме 21, функции распределения обладают следующими свойствами:
Свойство 8.
В любой точке  разница
разница  равна
равна 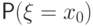 .
Иначе говоря,
.
Иначе говоря, 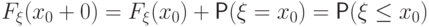 .
.
Это свойство получается аналогично свойствам (F2) и (F3)).
Разница  между пределом
при стремлении к
между пределом
при стремлении к  справа и значением в точке
справа и значением в точке  есть
величина скачка функции распределения. Эта величина равна нулю, если функция
распределения непрерывна (справа) в точке
есть
величина скачка функции распределения. Эта величина равна нулю, если функция
распределения непрерывна (справа) в точке  . Слева
функция распределения непрерывна всегда.
. Слева
функция распределения непрерывна всегда.
Замечание
Очень часто функцией распределения называют  . Эта
функция
отличается от определенной выше лишь тем, что она непрерывна
справа,
а не слева. И вероятность
. Эта
функция
отличается от определенной выше лишь тем, что она непрерывна
справа,
а не слева. И вероятность 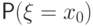 для нее равна
величине скачка слева, а не справа.
для нее равна
величине скачка слева, а не справа.
Свойство 9.
Для любой случайной величины 

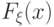 непрерывна в точках
непрерывна в точках  и
и  , то
, то
Доказательство.
Разобьем событие 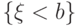 в объединение несовместных событий:
в объединение несовместных событий: 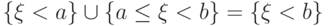 .
По свойству аддитивности вероятности,
.
По свойству аддитивности вероятности,
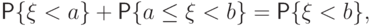
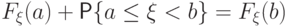 , что и требовалось доказать.
, что и требовалось доказать.Функция распределения дискретного распределения.
Согласно определению дискретного распределения, его функция распределения может быть найдена по таблице распределения так:
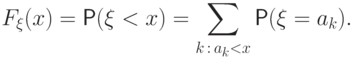
Из свойств 8 и 9 вытекает следующее свойство.
Свойство 10.
Случайная величина  имеет дискретное распределение тогда
и только тогда, когда функция распределения
имеет дискретное распределение тогда
и только тогда, когда функция распределения 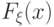 имеет
в точках
имеет
в точках  скачки с величиной
скачки с величиной 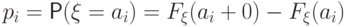 ,
и растет только за счет скачков.
,
и растет только за счет скачков.
