Элементарная теория вероятностей
Геометрическая вероятность
Рассмотрим какую-нибудь область  в
в 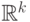 (на
прямой, на плоскости, в пространстве). Предположим, что
"мера"
(на
прямой, на плоскости, в пространстве). Предположим, что
"мера"  (длина, площадь, объем соответственно)
конечна.
Пусть случайный эксперимент состоит в том, что мы наудачу
бросаем в эту область точку.
Термин "наудачу" означает, что
вероятность попадания точки в любую часть
(длина, площадь, объем соответственно)
конечна.
Пусть случайный эксперимент состоит в том, что мы наудачу
бросаем в эту область точку.
Термин "наудачу" означает, что
вероятность попадания точки в любую часть 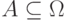 не
зависит от формы или расположения
не
зависит от формы или расположения 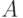 внутри
внутри  , а
зависит лишь от "меры" области
, а
зависит лишь от "меры" области  . Для такого
эксперимента вероятности определяются согласно
геометрическому определению вероятности:
. Для такого
эксперимента вероятности определяются согласно
геометрическому определению вероятности:
 |
( 2.3) |
Если для точки, брошенной в область  , выполнены
условия геометрического определения вероятности, то говорят,
что точка равномерно распределена
в области
, выполнены
условия геометрического определения вероятности, то говорят,
что точка равномерно распределена
в области  .
.
Пример 18.
Точка наудачу бросается на отрезок ![[0,\,1]](/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png) . Вероятность ей попасть
в точку
. Вероятность ей попасть
в точку 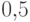 равна нулю, так как равна нулю
мера множества, состоящего из одной точки ("длина точки").
Но попадание в точку
равна нулю, так как равна нулю
мера множества, состоящего из одной точки ("длина точки").
Но попадание в точку 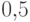 не является
невозможным событием - это один из элементарных исходов.
не является
невозможным событием - это один из элементарных исходов.
Пример 19.
Точка наудачу бросается в круг c единичным радиусом. Найти вероятность того,
что расстояние 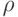 до точки от центра круга будет меньше заданного
числа
до точки от центра круга будет меньше заданного
числа 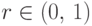 .
.
Решение.
Интересующее нас событие  происходит, когда точка
попадает
во внутренний круг с радиусом
происходит, когда точка
попадает
во внутренний круг с радиусом 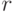 и тем же центром.
По формуле (2.3), вероятность
этого события равна отношению площадей кругов:
и тем же центром.
По формуле (2.3), вероятность
этого события равна отношению площадей кругов:
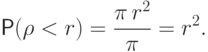
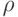 до брошенной в круг точки
распределено не равномерно на отрезке
до брошенной в круг точки
распределено не равномерно на отрезке ![[0,\,1]](/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png) . Для равномерного
распределения мы получили бы вероятность
. Для равномерного
распределения мы получили бы вероятность 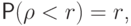 а
не
а
не 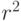 .
.Пример 20. (задача о встрече)
Два человека 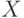 и
и 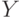 условились встретиться
в определенном месте между двумя и тремя часами дня.
Пришедший первым ждет другого в течение
условились встретиться
в определенном месте между двумя и тремя часами дня.
Пришедший первым ждет другого в течение  минут,
после чего уходит. Чему равна вероятность встречи этих лиц,
если каждый из них может прийти в любое время в течение указанного часа
независимо от другого?
минут,
после чего уходит. Чему равна вероятность встречи этих лиц,
если каждый из них может прийти в любое время в течение указанного часа
независимо от другого?
Решение.
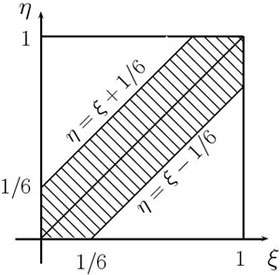
Будем считать интервал от двух до трех часов дня
отрезком ![[0,\,1]](/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png) . Обозначим
через
. Обозначим
через ![\xi\in[0,\,1]](/sites/default/files/tex_cache/cbfded2432f7a9afe043f144dd0fc39d.png) и
и ![\eta\in[0,\,1]](/sites/default/files/tex_cache/ba4dafb37bf4576ef206199fe6bc3fa5.png) моменты
прихода
моменты
прихода 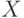 и
и 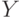 в течение этого часа (
рис.
2.2).
Результатами эксперимента
являются всевозможные пары точек
в течение этого часа (
рис.
2.2).
Результатами эксперимента
являются всевозможные пары точек 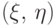 из единичного
квадрата:
из единичного
квадрата:
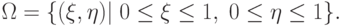
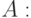
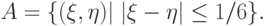
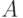 наудачу брошенной в квадрат точки
означает, что
наудачу брошенной в квадрат точки
означает, что 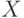 и
и 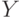 встретятся.
встретятся.Тогда вероятность встречи равна отношению площадей
множеств 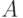 и
и  :
:
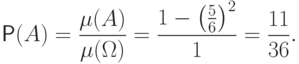
Существование неизмеримых множеств. Заканчивая обсуждение понятия геометрической вероятности, отметим следующее неприятное обстоятельство.
Если даже эксперимент удовлетворяет геометрическому определению
вероятности, далеко не для всех множеств 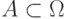 вероятность
может быть вычислена как отношение меры
вероятность
может быть вычислена как отношение меры 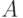 к
мере
к
мере  . Причиной этого является существование
так называемых "неизмеримых" множеств, т.е. множеств,
мера которых не существует.
. Причиной этого является существование
так называемых "неизмеримых" множеств, т.е. множеств,
мера которых не существует.
Пример 21. (множество Витали) В этом примере мы построим множество на отрезке, "длина" которого не существует. Нам понадобятся лишь следующие очевидные свойства "длины" множества: длина множества остается неизменной при сдвиге всех точек этого множества; длина множества, составленного из счетного объединения попарно непересекающихся множеств, равняется сумме длин этих множеств.
Рассмотрим окружность с радиусом 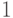 (то же, что
отрезок
(то же, что
отрезок ![[0,2\pi]\text{).}](/sites/default/files/tex_cache/ca96231fab6a72eb503bc18a40636db4.png) Возьмем любое иррациональное
число
Возьмем любое иррациональное
число  . Поскольку оно иррационально,
число
. Поскольку оно иррационально,
число  не является
целым ни при каком целом
не является
целым ни при каком целом 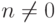 . Поэтому если взять {произвольную}
точку (угол)
. Поэтому если взять {произвольную}
точку (угол) ![x\in[0,2\pi]](/sites/default/files/tex_cache/d1ef288612e901a2bce595af3119db70.png) на окружности и перечислить все точки,
которые получаются поворотом
на окружности и перечислить все точки,
которые получаются поворотом 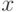 на угол
на угол  , где
, где 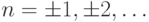 , то мы ни разу не вернемся в
точку
, то мы ни разу не вернемся в
точку  . Точек, получившихся
из
. Точек, получившихся
из 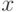 такими поворотами, счетное число.
Объединим их в один класс. С любой другой точкой окружности
можно тоже связать класс точек, получающихся из нее поворотами
на
такими поворотами, счетное число.
Объединим их в один класс. С любой другой точкой окружности
можно тоже связать класс точек, получающихся из нее поворотами
на  при целых
при целых  . Эти классы либо совпадают,
либо не имеют
общих точек. Таким образом, вся окружность разбивается
на классы точек. В каждом классе
счетное число точек, и все точки в одном классе получаются друг из друга
такими поворотами. Разные классы не пересекаются. Заметим, что
классов несчетное число, т.к. объединением счетного числа
счетных множеств нельзя получить несчетное число точек окружности.
. Эти классы либо совпадают,
либо не имеют
общих точек. Таким образом, вся окружность разбивается
на классы точек. В каждом классе
счетное число точек, и все точки в одном классе получаются друг из друга
такими поворотами. Разные классы не пересекаются. Заметим, что
классов несчетное число, т.к. объединением счетного числа
счетных множеств нельзя получить несчетное число точек окружности.
Искомое множество 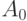 определим так: возьмем из каждого такого
класса
ровно по одной точке.
Пусть множество
определим так: возьмем из каждого такого
класса
ровно по одной точке.
Пусть множество  получается поворотом всех точек
множества
получается поворотом всех точек
множества 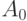 на угол
на угол  ,
, 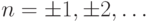 Так как все точки одного класса можно получить, поворачивая
любую
из них на угол
Так как все точки одного класса можно получить, поворачивая
любую
из них на угол 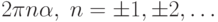 , а в
множестве
, а в
множестве 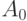 собрано по одной точке из каждого класса,
то, поворачивая это множество, получим все точки окружности.
Предположим, что
"длина"
собрано по одной точке из каждого класса,
то, поворачивая это множество, получим все точки окружности.
Предположим, что
"длина" 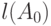 множества
множества 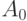 существует.
Тогда все множества
существует.
Тогда все множества  имеют ту же длину,
так как получены из
имеют ту же длину,
так как получены из 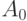 поворотом. Но все эти множества
не пересекаются, поэтому "длина" их объединения равна сумме их длин
и равна длине отрезка
поворотом. Но все эти множества
не пересекаются, поэтому "длина" их объединения равна сумме их длин
и равна длине отрезка ![[0,2\pi] :](/sites/default/files/tex_cache/e9c63d95ce2a675eb6f572003c12e2b9.png)
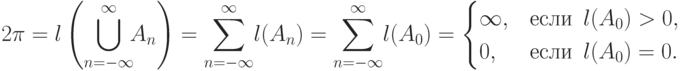
Полученное противоречие означает, что
длина множества 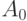 просто не существует.
просто не существует.
Итак, мы построили множество на отрезке, длина которого не существует
(неизмеримое множество).
Пользуясь геометрическим определением вероятности,
мы не можем определить вероятность попадания точки в такое неизмеримое
множество.
Но если не для любого 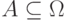 мы можем определить
вероятность,
следует сузить класс множеств, называемых "событиями", оставив
в этом классе только те множества, вероятность которых
определена.
мы можем определить
вероятность,
следует сузить класс множеств, называемых "событиями", оставив
в этом классе только те множества, вероятность которых
определена.
В следующей лекции мы изучим предложенную А.Н.Колмогоровым
аксиоматику теории вероятностей: познакомимся с
понятиями 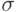 -алгебры (или поля) событий, вероятностной меры и
вероятностного пространства.
-алгебры (или поля) событий, вероятностной меры и
вероятностного пространства.