Основные семейства распределений
Гамма-распределение.
Говорят, что  имеет
гамма-распределение с параметрами
имеет
гамма-распределение с параметрами 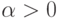 ,
, 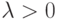 ,
и пишут:
,
и пишут:  ,
если
,
если  имеет следующую плотность распределения:
имеет следующую плотность распределения:
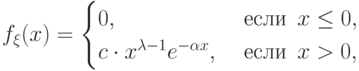
 вычисляется из свойства (f2) плотности так:
вычисляется из свойства (f2) плотности так: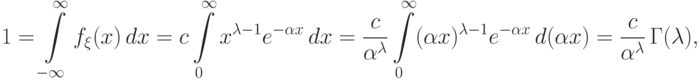
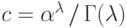 .
Здесь через
.
Здесь через  обозначен интеграл
обозначен интеграл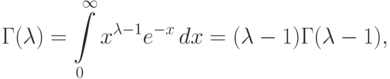
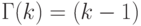 !
при целых положительных
!
при целых положительных 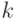 ,
, 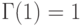 . Замена в
интеграле Пуассона даст
. Замена в
интеграле Пуассона даст  .
.Полезно отметить, что показательное распределение есть частный случай
гамма распределения: 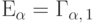 .
.
Функцию распределения гамма-распределения можно записать, вообще говоря, только в виде интеграла:
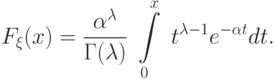
Распределение Коши.
Говорят, что  имеет
распределение Коши с параметрами
имеет
распределение Коши с параметрами 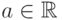 ,
,  ,
и пишут:
,
и пишут: 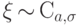 ,
если
,
если  имеет следующую плотность распределения:
имеет следующую плотность распределения:
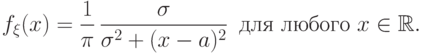
Плотность распределения Коши симметрична относительно прямой  и похожа на плотность нормального распределения, но имеет
более толстые "хвосты"
на
и похожа на плотность нормального распределения, но имеет
более толстые "хвосты"
на  . Функция распределения случайной величины
. Функция распределения случайной величины  с распределением Коши
равна
с распределением Коши
равна 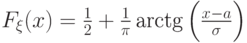 при всех
при всех 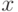 .
.
Распределение Парето.
Говорят, что  имеет
распределение Парето с параметром
имеет
распределение Парето с параметром 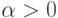 ,
если
,
если  имеет следующие плотность и функцию распределения:
имеет следующие плотность и функцию распределения:

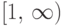 , а на
, а на 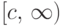 при
при  .
.С другими абсолютно непрерывными распределениями (хи-квадрат Пирсона, распределениями Стьюдента, Фишера, Колмогорова, Лапласа, Вейбулла, логарифмически нормальным и некоторыми другими) читатель познакомится при изучении математической статистики.
Свойства нормального распределения.
Рассмотрим отдельно свойства самого главного распределения.
Сначала установим связь между функциями 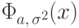 и
и 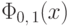 .
.
Свойство 14.
Для любого 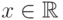 справедливо соотношение:
справедливо соотношение:

Доказательство. Действительно,
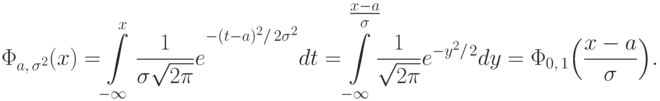
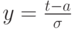 ,
, 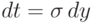 ,
верхняя граница интегрирования
,
верхняя граница интегрирования 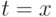 при такой замене перешла в
при такой замене перешла в 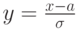 .
.То же самое для случайных величин можно сформулировать так:
Следствие 2.
Если  , то
, то 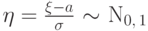 .
.
Доказательство. Убедимся, что случайная величина 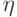 имеет функцию
распределения
имеет функцию
распределения 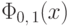 :
:
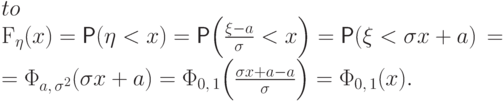
Следствие 3.
Если  , то
, то
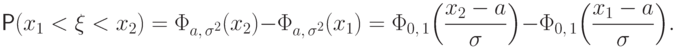
Видим, что вычисление любых вероятностей для нормально распределенной
случайной величины сводится к вычислению функции распределения 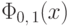 .
Она обладает следующими свойствами ( нарисуйте их на
графике
плотности стандартного нормального распределения ).
.
Она обладает следующими свойствами ( нарисуйте их на
графике
плотности стандартного нормального распределения ).
Свойство 15. 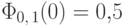 ,
, 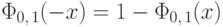 .
.
Свойство 16.
Если 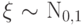 , то для любого
, то для любого 
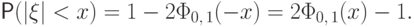
Доказательство. При  имеем
имеем
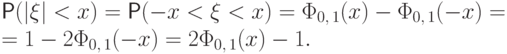
Свойство 17. (Правило трех сигм)
Если  , то
, то
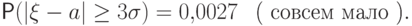
Доказательство. Перейдем к противоположному событию:
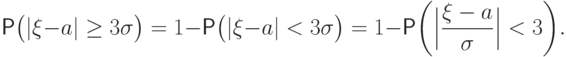
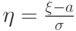 имеет
стандартное нормальное
распределение и можно использовать свойство 16
имеет
стандартное нормальное
распределение и можно использовать свойство 16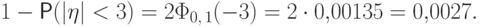
 полезно отыскать в таблице.
полезно отыскать в таблице.Большого смысла в запоминании числа 0,0027 нет, но полезно помнить,
что почти вся масса нормального распределения сосредоточена
в границах от 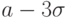 до
до 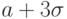 .
.

