Аксиоматика теории вероятностей
То же самое еще раз и подробно:
Определение 10.
Пусть  - пространство элементарных исходов,
- пространство элементарных исходов, 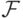 -
-  -алгебра его подмножеств
(событий).
Вероятностью или вероятностной
мерой на
-алгебра его подмножеств
(событий).
Вероятностью или вероятностной
мерой на 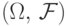 называется функция
называется функция 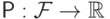 , обладающая свойствами:
, обладающая свойствами:
(P1) 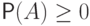 для любого события
для любого события 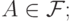
(P2) для любого счетного набора попарно несовместных
событий 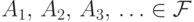 имеет место
равенство
имеет место
равенство
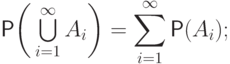
(P3) вероятность достоверного события равна единице: 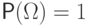 .
.
Свойства (P1) - (P3) называют аксиомами вероятности.
Определение 11.
Тройка 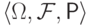 ,
в которой
,
в которой  - пространство элементарных исходов,
- пространство элементарных исходов, 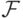 -
-  -алгебра его подмножеств и
-алгебра его подмножеств и 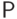 -
вероятностная мера на
-
вероятностная мера на 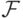 , называется вероятностным
пространством.
, называется вероятностным
пространством.
Докажем свойства вероятности, вытекающие из аксиом. Ниже мы не будем всякий раз оговаривать, что имеем дело только с событиями.
Теорема 8. Вероятность обладает следующими свойствами.
-
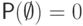 .
. - Для любого конечного
набора попарно несовместных событий
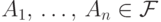 имеет место равенство:
имеет место равенство:
-
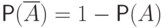 .
. - Если
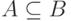 , то
, то 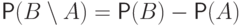 .
. - Если
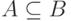 , то
, то 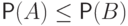 (монотонность вероятности).
(монотонность вероятности). -
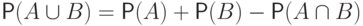 .
. -
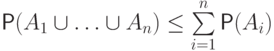 .
. - Формула включения-исключения
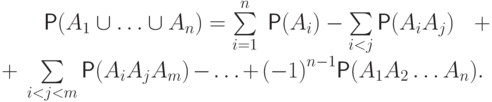
( 3.1)
Доказательство.
- События
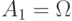 ,
, 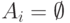 , где
, где 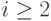 , попарно несовместны, и
их объединение есть
, попарно несовместны, и
их объединение есть  . По аксиоме (P2),Это возможно только в случае
. По аксиоме (P2),Это возможно только в случае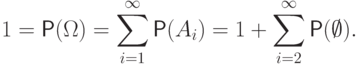
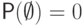 .
. - Положим
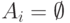 при любом
при любом  .
События
.
События 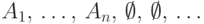 попарно несовместны, и по аксиоме (P2),
попарно несовместны, и по аксиоме (P2),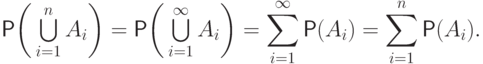
- Событие
 равно объединению двух
несовместных событий:
равно объединению двух
несовместных событий: 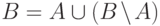 . Согласно свойству 2,
. Согласно свойству 2, 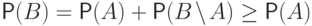 .
. - Событие
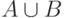 можно разложить в объединение двух
несовместных событий
можно разложить в объединение двух
несовместных событий 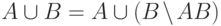 ,
причем
,
причем 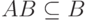 . По свойствам 2 и 4 получим
. По свойствам 2 и 4 получим 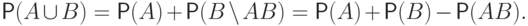
- При
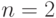 неравенство вытекает из свойства 6:
неравенство вытекает из свойства 6:
Упражнение. Докажите свойство 7 и формулу (3.1) с помощью математической индукции.
Приведем пример задачи, в которой использование формулы включения-исключения - самый простой путь решения.
Пример 28. (задача о рассеянной секретарше)
Есть  писем и
писем и  подписанных конвертов. Письма
раскладываются
в конверты наудачу по одному. Найти вероятность того, что хотя бы одно
письмо попадет в предназначенный ему конверт.
подписанных конвертов. Письма
раскладываются
в конверты наудачу по одному. Найти вероятность того, что хотя бы одно
письмо попадет в предназначенный ему конверт.
Решение. Пусть
событие  ,
, 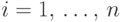 ,
означает, что
,
означает, что  -е письмо попало в свой конверт.
Тогда
-е письмо попало в свой конверт.
Тогда
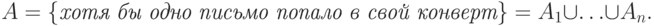
Cобытия 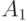 ,
,  ,
, 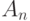 совместны,
поэтому используем
формулу (3.1). По классическому
определению вероятности
вычислим вероятности всех событий
совместны,
поэтому используем
формулу (3.1). По классическому
определению вероятности
вычислим вероятности всех событий  и их пересечений.
Элементарными исходами будут всевозможные
перестановки
и их пересечений.
Элементарными исходами будут всевозможные
перестановки  писем по
писем по  конвертам.
Их общее число есть
конвертам.
Их общее число есть 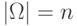 !,
и событию
!,
и событию  благоприятны
благоприятны 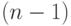 ! из них, а именно
перестановки всех писем, кроме
! из них, а именно
перестановки всех писем, кроме  -го, лежащего в своем конверте.
Поэтому
-го, лежащего в своем конверте.
Поэтому 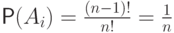 - одна и та
же
для всех
- одна и та
же
для всех  .
Точно так же
.
Точно так же
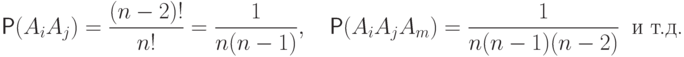
Вычислим количество слагаемых в каждой сумме в формуле (3.1).
Например, сумма по 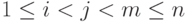 состоит из
состоит из 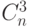 слагаемых - ровно столько троек индексов можно
образовать из
слагаемых - ровно столько троек индексов можно
образовать из  номеров событий.
Подставляя все вероятности в формулу (3.1), получаем:
номеров событий.
Подставляя все вероятности в формулу (3.1), получаем:
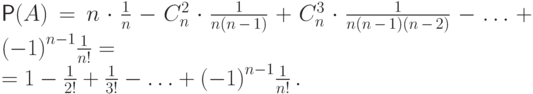 |
( 3.2) |
Упражнение.
Выписать разложение 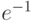 в ряд Тейлора и убедиться в том, что
в ряд Тейлора и убедиться в том, что  при
при 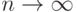 .
.
