Аксиоматика теории вероятностей
Свойство 3.
Всякая  -алгебра является алгеброй.
-алгебра является алгеброй.
Доказательство.
Пусть 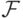 -
-  -алгебра.
Нужно проверить, что она удовлетворяет свойству (A3), т.е.
для любых
-алгебра.
Нужно проверить, что она удовлетворяет свойству (A3), т.е.
для любых 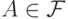 и
и 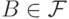 выполняется
выполняется  .
.
Превратим пару  в счетную последовательность событий так:
в счетную последовательность событий так: 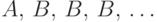 , т.е. положим
, т.е. положим 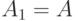 ,
, 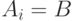 при всех
при всех 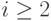 .
Объединение
.
Объединение 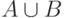 совпадает с объединением
всех множеств
совпадает с объединением
всех множеств  из этой бесконечной последовательности. А так
как
из этой бесконечной последовательности. А так
как 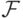 -
-  -алгебра, то
-алгебра, то
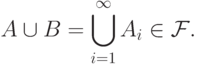
Итак, всякая  -алгебра автоматически является алгеброй,
но не наоборот.
Приведем пример алгебры, не являющейся
-алгебра автоматически является алгеброй,
но не наоборот.
Приведем пример алгебры, не являющейся  -алгеброй.
-алгеброй.
Пример 23.
Пусть 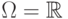 , и пусть
, и пусть 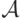 -
множество, содержащее любые
конечные подмножества
-
множество, содержащее любые
конечные подмножества  (т.е. состоящие из конечного числа
точек, в том числе пустое)
и их дополнения. Так, множество
(т.е. состоящие из конечного числа
точек, в том числе пустое)
и их дополнения. Так, множество 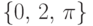 принадлежит
принадлежит 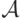 , множество
, множество 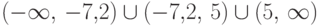 не принадлежит
не принадлежит 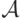 .
.
Легко проверить, что множество 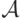 является алгеброй.
Действительно, пустое множество и само
является алгеброй.
Действительно, пустое множество и само 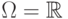 там
содержатся,
дополнение к любому конечному подмножеству множества вещественных
чисел содержится в
там
содержатся,
дополнение к любому конечному подмножеству множества вещественных
чисел содержится в 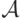 по определению,
дополнение к множеству вида
по определению,
дополнение к множеству вида 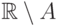 для конечных
для конечных  совпадает
с
совпадает
с  и также принадлежит
и также принадлежит 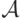 по определению.
Свойство (A3)
проверяется непосредственно: объединение любых конечных множеств снова конечно
и поэтому принадлежит
по определению.
Свойство (A3)
проверяется непосредственно: объединение любых конечных множеств снова конечно
и поэтому принадлежит 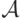 . Объединение конечного множества
с множеством вида
. Объединение конечного множества
с множеством вида 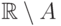 , где
, где  конечно,
есть снова множество
вида
конечно,
есть снова множество
вида  , где
, где  конечно (или пусто) и
т.д.
конечно (или пусто) и
т.д.
Однако алгебра 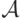 не содержит ни одного счетного
множества
точек. Действительно, объединяя конечные множества в конечном числе, мы можем
получить только конечное множество. Например, натуральный ряд
не содержит ни одного счетного
множества
точек. Действительно, объединяя конечные множества в конечном числе, мы можем
получить только конечное множество. Например, натуральный ряд 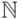 не принадлежит
не принадлежит 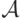 . Поэтому
. Поэтому 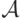 не
является
не
является  -алгеброй:
для бесконечной, но счетной последовательности одноточечных множеств
-алгеброй:
для бесконечной, но счетной последовательности одноточечных множеств  из
из 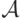 их объединение
их объединение 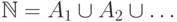 не
принадлежит
не
принадлежит 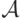 .
.
Все алгебры из примера 22 являются  -алгебрами, поскольку
содержат лишь конечное число элементов. Вообще, на конечном множестве
-алгебрами, поскольку
содержат лишь конечное число элементов. Вообще, на конечном множестве  понятия алгебры и
понятия алгебры и  -алгебры совпадают.
Множество
всех подмножеств
-алгебры совпадают.
Множество
всех подмножеств  является
является  -алгеброй для
любого
-алгеброй для
любого  .
.
Борелевская  -алгебра.
Приведем еще один
пример
-алгебра.
Приведем еще один
пример  -алгебры, которая
нам будет необходима в дальнейшем,-
-алгебры, которая
нам будет необходима в дальнейшем,-  -алгебры
борелевских множеств на вещественной прямой.
-алгебры
борелевских множеств на вещественной прямой.
Борелевской сигма-алгеброй в  называется самая
маленькая среди
всех возможных
называется самая
маленькая среди
всех возможных  -алгебр, содержащих любые интервалы на
прямой.
Разумеется,
-алгебр, содержащих любые интервалы на
прямой.
Разумеется,  -алгебры, содержащие все интервалы, существуют.
Например,
множество всех подмножеств
-алгебры, содержащие все интервалы, существуют.
Например,
множество всех подмножеств  - это
- это  -алгебра, и
она содержит все интервалы. Что же такое "самая маленькая
-алгебра, и
она содержит все интервалы. Что же такое "самая маленькая  -алгебра"
из нескольких данных? Обратимся к примерам.
-алгебра"
из нескольких данных? Обратимся к примерам.
Пусть 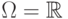 - вещественная прямая.
Рассмотрим некоторые наборы множеств, не являющиеся
- вещественная прямая.
Рассмотрим некоторые наборы множеств, не являющиеся  -алгебрами, и увидим, как их можно дополнить до
-алгебрами, и увидим, как их можно дополнить до  -алгебр.
-алгебр.
Пример 24.
Множество ![\mathfrak A = \{\mathbb R,\, \emptyset,\, [0,\,1],\,
\{ 0\}\}](/sites/default/files/tex_cache/2cb3b4c3bc73503d9cbcd271a290a6a1.png) не является
не является  -алгеброй, так как,
например,
-алгеброй, так как,
например,  .
Самый маленький набор множеств, содержащий
.
Самый маленький набор множеств, содержащий  и
являющийся
и
являющийся  -алгеброй (минимальная
-алгеброй (минимальная  -алгебра),
получится, если включить в него всевозможные
объединения, пересечения и дополнения множеств из
-алгебра),
получится, если включить в него всевозможные
объединения, пересечения и дополнения множеств из  :
:
![\mathcal F =\{\,\mathbb R, \emptyset,\ [0,\,1],\ \{
0\},\
(-\infty,\,0)\cup(1,\,\infty),\, (0,\,1],\\ (-\infty,\,0]\cup(1,\,\infty),\,
(-\infty,\,0)\,\cup\,(0,\,\infty)\}.](/sites/default/files/tex_cache/94790c339c85ded71b1b8f8c28875a8d.png)
Определение 6.
Минимальной  -алгеброй, содержащей
набор множеств
-алгеброй, содержащей
набор множеств  , называется пересечение
всех
, называется пересечение
всех  -алгебр, содержащих
-алгебр, содержащих  .
.
Еще раз напомним, что пересекать в определении 6 есть что: хотя бы одна  -алгебра, содержащая данный набор множеств, всегда найдется
- это
-алгебра, содержащая данный набор множеств, всегда найдется
- это  -алгебра всех подмножеств
-алгебра всех подмножеств  .
.
Упражнение. Доказать, что пересечение двух  -алгебр, содержащих
набор множеств
-алгебр, содержащих
набор множеств  , снова является
, снова является  -алгеброй, содержащей
-алгеброй, содержащей  .
.
Упражнение.
Найти минимальную  -алгебру, содержащую следующий набор
подмножеств
-алгебру, содержащую следующий набор
подмножеств  :
: ![\mathfrak A = \left\{ \mathbb R,\, \emptyset,\, [0,\,1],\,
\{3\} \right\}](/sites/default/files/tex_cache/cefc1ad9a3c8326c2a0760e8807edcef.png) .
.
Дадим определение борелевской сигма-алгебры. Пусть по-прежнему 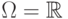 ,
а множество
,
а множество  состоит из всевозможных открытых
интервалов
состоит из всевозможных открытых
интервалов 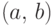 , где
, где  :
:  .
Это множество всех интервалов не является ни алгеброй, ни
.
Это множество всех интервалов не является ни алгеброй, ни  -алгеброй.
-алгеброй.
Определение 7.
Минимальная  -алгебра, содержащая множество
-алгебра, содержащая множество  всех интервалов на вещественной прямой,
называется борелевской
всех интервалов на вещественной прямой,
называется борелевской  -алгеброй в
-алгеброй в  и обозначается
и обозначается 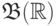 .
.
Перечислим некоторые множества на прямой, содержащиеся
в 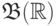 по определению.
Таковы все привычные нам множества. Чтобы получить
множество, не содержащееся в
по определению.
Таковы все привычные нам множества. Чтобы получить
множество, не содержащееся в 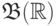 , требуются специальные
построения.
Итак, мы знаем, что все интервалы на прямой принадлежат
, требуются специальные
построения.
Итак, мы знаем, что все интервалы на прямой принадлежат 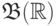 ,
и
,
и 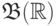 -
-  -алгебра. Отсюда сразу
следует, что
-алгебра. Отсюда сразу
следует, что 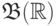 содержит любое множество,
которое можно получить из интервалов с помощью счетного числа операций
объединения
или пересечения, а также взятием дополнения.
содержит любое множество,
которое можно получить из интервалов с помощью счетного числа операций
объединения
или пересечения, а также взятием дополнения.
В частности, 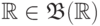 по свойству
(S1). Далее, все одноточечные множества
по свойству
(S1). Далее, все одноточечные множества  , где
, где 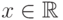 , принадлежат
, принадлежат 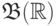 . Действительно,
интервалы
. Действительно,
интервалы 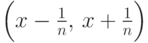 принадлежат
принадлежат 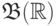 ,
по определению,
при любом
,
по определению,
при любом  . Их счетное пересечение также принадлежит
. Их счетное пересечение также принадлежит 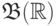 по свойству (S4):
по свойству (S4):
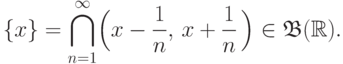
Далее, любой интервал вида ![(a,\,b\,]](/sites/default/files/tex_cache/ceb0c3db30ce97241b738bc089b67f0a.png) (или
(или 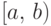 , или
, или ![[a,\,b\,]](/sites/default/files/tex_cache/d81e28b6c2ffcbd7ae9efd42310804bf.png) ),
где
),
где  , принадлежит
, принадлежит 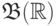 как объединение
открытого интервала
и точки (или двух точек):
как объединение
открытого интервала
и точки (или двух точек): ![(a,\,b\,]=(a,\,b)\cup \{b\}](/sites/default/files/tex_cache/8c8617c69385b2116b66f26e78317110.png) .
.
Упражнение.
Докажите, что
множество натуральных чисел 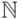 и множество рациональных чисел
и множество рациональных чисел  принадлежат
принадлежат 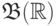 .
.
Борелевская  -алгебра в
-алгебра в 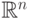 строится
совершенно
так же, как в
строится
совершенно
так же, как в  . Это должна быть минимальная
. Это должна быть минимальная  -алгебра, содержащая все множества
вида
-алгебра, содержащая все множества
вида  - уже не
интервалы, как в
- уже не
интервалы, как в  ,
а прямоугольники в
,
а прямоугольники в  , параллелепипеды в
, параллелепипеды в 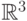 и т.д.
Вместе с ними
и т.д.
Вместе с ними  содержит
любые множества, являющиеся "предельными" для объединений
измельчающихся
прямоугольников. Например, круг в
содержит
любые множества, являющиеся "предельными" для объединений
измельчающихся
прямоугольников. Например, круг в  является борелевским
множеством -
можно изнутри или снаружи приблизить его объединениями прямоугольников.
является борелевским
множеством -
можно изнутри или снаружи приблизить его объединениями прямоугольников.
Итак, мы определили специальный класс 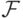 подмножеств
подмножеств  , названный
, названный  -алгеброй событий.
Применение счетного числа любых операций
(объединений, пересечений, дополнений)
к множествам из
-алгеброй событий.
Применение счетного числа любых операций
(объединений, пересечений, дополнений)
к множествам из 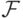 снова дает множество
из
снова дает множество
из 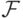 , т.е. не выводит за рамки этого класса.
Событиями будем называть только множества
, т.е. не выводит за рамки этого класса.
Событиями будем называть только множества 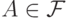 .
.
Определим теперь понятие вероятности как функции, определенной на множестве событий (функции, которая каждому событию ставит в соответствие число - вероятность этого события).
