НОУ ИНТУИТ | Эволюционные вычисления. Лекция 12: Муравьиные алгоритмы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет путей сообщения

Опубликован: 10.10.2014 | Доступ: свободный | Студентов: 866 / 193 | Длительность: 22:10:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист, Архитектор программного обеспечения

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

12.2. Простой муравьиный алгоритм

Первые муравьиные алгоритмы, разработанные в [1], относятся по современной классификации к "муравьиным системам" (antsystems), которые будут изложены ниже. Сначала мы рассмотрим (исключительно в учебных целях) простой муравьиный алгоритм (ПМА) (simple ant colony optimization -SACO), в котором фактически формализованы приведенные выше экспериментальные исследования и представлены основные аспекты муравьиных алгоритмов (МА) [2].

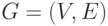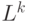В качестве иллюстрации возьмем задачу поиска кратчайшего пути между двумя узлами графа G=(V,E) , где – множество узлов (вершин), а – матрица, которая представляет связи между узлами. Пусть n_G=|V| - число узлов в графе. Обозначим L^k – длину пути в графе, пройденного -м муравьем, которая равна числу пройденных дуг (ребер) от первой до последней вершины пути. Пример графа с выделенным путем представлен на рис.12.7. 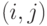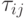С каждой дугой, соединяющей вершины (i,j) , ассоциируем концентрацию феромона $\tau_{ij}$ .

Рис. 12.7. Пример графа.

Строго говоря, в начальный момент времени концентрация феромона для каждой дуги графа нулевая, но мы для удобства каждой дуге присвоим небольшое случайное число 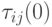$\tau_{ij}(0)$ .

Муравей выбирает следующую дугу пути случайным образом в фактически в соответствии с алгоритмом 12.1 следующим образом. Множество муравьев 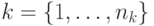$k=\{1,…,n_k\}$ помещаются в начальную вершину. В каждой итерации ПМА каждый муравей пошагово строит путь до конечной вершины. При этом в каждой вершине каждый муравей должен выбрать следующую дугу пути. 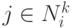Если -ймуравей находится в -ой вершине,то он выбирает следующую вершину $j\in N_i^k$ на основе вероятностей перехода

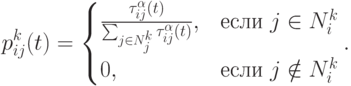$p_{ij}^k(t)=\begin{cases}\frac{\tau_{ij}^{\alpha}(t)}{\sum_{j\in N_j^k} \tau_{ij}^{\alpha}(t)},&\mbox{если $j\in N_i^k$}\\0,&\mbox{если $j\notin N_i^k$}\end{cases}.$

( 12.2)

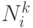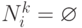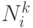Здесь N_i^k представляет множество возможных вершин, связанных с -й вершиной, для -го муравья. Если для любого -го узла и -го муравья $N_i^k=\varnothing$ , тогда предшественник узла включается в N_i^k . В этом случае в пути возможны петли. Эти петли удаляются при достижении конечного города пути. В (12.2) $\alpha$ - положительная константа, которая определяет влияние концентрации феромона. Очевидно большие значения $\alpha$ повышают влияние концентрации феромона. Это особенно существенно в начальной стадии для начальных случайных значений концентрации, что может привести к преждевременной сходимости к субоптимальным решениям. Когда все муравьи построили полный путь от начальной до конечной вершины, удаляются петли в путях, и каждый муравей помечает свой построенный путь, откладывая для каждой дуги феромон в соответствии со следующей формулой

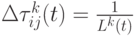$\Delta\tau_{ij}^k(t)=\frac{1}{L^k(t)}$

( 12.3)

Здесь 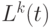L^k(t) – длина пути, построенного -м муравьем в момент времени .

Таким образом, для каждой дуги графа концентрация феромона определяется следующим образом

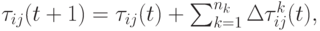$\tau_{ij}(t+1)=\tau_{ij}(t)+\sum_{k=1}^{n_k}\Delta\tau_{ij}^k(t),$

( 12.4)

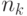где n_k - число муравьев. Из (12.3) следует, что общая концентрация феромона для данной дуги пропорциональна "качеству" путей, в которые входит эта дуга, поскольку откладываемое количество феромона согласно (12.3) отражает "качество" соответствующего пути. В данном случае "качество" обратно пропорционально длине пути (числу дуг, вошедших в путь). Но в общем случае может быть использована и другая мера качества (например, стоимость проезда по данному пути или геометрическое расстояние и т.п.). Пусть 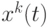x^k(t) обозначает решение в момент , и некоторая функция f(x^k(t)) выражает качество решения. 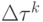Если $\Delta\tau^k$ не пропорционально качеству решения и все муравьи откладывают одинаковое количество феромона 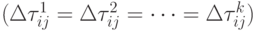$(\Delta\tau_{ij}^1=\Delta\tau_{ij}^2=\dots=\Delta\tau_{ij}^k)$ , то существует только один фактор, который зависит от длины пути и способствует выбору коротких путей. Это ведет к двум основным способам оценки качества решений, которые используются в МА:

неявная оценка, где муравьи используют отличие в длине путей относительно построенных путей другими муравьями;
явная оценка, количество феромона пропорционально некоторой мере качества построенного решения.

В нашем случае мы имеем явную оценку качества решения согласно (12.3), которая ведет к тому, что дуги, входящие в длинные пути, становятся менее привлекательными для окончательных решений.

В алгоритме А12.2 [2] могут быть использованы различные критерии окончания, например,

окончание при превышении заданного числа итераций;
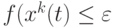окончание по найденному приемлемому решению $f(x^k(t)\le\varepsilon$ ;
окончание, когда все муравьи следуют одним и тем же путем.

Компьютерные эксперименты с двумя мостами показали, что муравьи быстро находят решение и мало исследуют альтернативные варианты. Для предотвращения преждевременной сходимости и расширения пространства поиска можно ввести искусственное испарение феромона на каждой итерации алгоритма следующим образом:

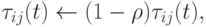$\tau_{ij}(t)\gets (1-\rho)\tau_{ij}(t),$

( 12.5)

где $\rho\in[0,1]$ . При этом константа $\rho$ определяет скорость испарения, которое заставляет муравьи "забывать" предыдущие решения. Очевидно, что при больших значениях $\rho$ феромон испаряется быстро, в то время как малые значения $\rho$ способствуют медленному испарению. Отметим, что чем больше испаряется феромон, тем поиск становится более случайным.

Так при $\rho=1$ мы имеем случайный поиск.

Следует отметить, построение решения является результатом совместного поведения, которое определяется простым поведением отдельных муравьев: каждый муравей выбирает следующий участок пути на основе информации, предоставляемой другими муравьями в форме отложений феромона. При этом при выборе муравей использует информацию только локального окружения.

Эксперименты (DorigoM., DiCaro [4]) показали, что:

ПМА работает хорошо для очень маленьких графов и в большинстве случаев находит кратчайший путь;
для больших графов характеристики ухудшаются, алгоритм становится менее стабильным и более чувствительным к выбору параметров;
сходимость к кратчайшему пути хорошая при малом числе муравьев, в то время как большое количество муравьев часто ведет к тому, что процесс поиска не сходится;
эффект испарения более важен для сложных графов. В этом случае при $\rho=0$ (нет испарения) алгоритм часто не сходится. С другой стороны, если феромон испаряется слишком быстро (большие значения $\rho$ ), алгоритм часто сходится к субоптимальным решениям;
при малых значениях $\alpha$ алгоритм в основном сходится к кратчайшему пути. Для сложных задач (высокой размерности) большое значение $\alpha$ ведет к плохой сходимости.

Эти исследования показали (как и для других эволюционных алгоритмов) важность проблемы эксплуатации-расширения пространства поиска. Характеристики ПМА можно значительно улучшить путем включения эвристической информации при выборе следующей дуги, запоминания локальной информации для предотвращения преждевременных циклов, использования различных значений коэффициентов на различных стадиях поиска.

Дальше >>

Авторизоваться

Эволюционные вычисления

Муравьиные алгоритмы

12.2. Простой муравьиный алгоритм

Вопросы и ответы