Генетическое программирование
Ниже вводятся различные способы кодирования (представления) программ: древовидное, линейное, графоподобное. Для них представлены соответствующие генетические операторы кроссинговера и мутации и виды фитнесс-функции. Описан метод символьной регрессии.
Эксперименты по компьютерному синтезу программ проводились с конца 50-х годов [1] и являлись одной из важнейших компонент машинного обучения, которое относится к одному из самых перспективных направлений искусственного интеллекта. В процессе обучения хромосомы или некоторые структуры автоматически генерируются с помощью генетических операторов и представляют компьютерные программы различной сложности. Первые эксперименты проводились с использованием двоичных кодов программ и показали скромные результаты, обусловленные, в первую очередь, состоянием вычислительной техники и программного обеспечения (ПО) того времени. И только в 80-х годах с развитием достаточно мощной компьютерной техники и ПО сформировалось генетическое программирование (ГП), в первую очередь на основе работ Koza [2].
В генетическом программировании (ГП) в качестве особи выступает программа, представленная в определенном формате, которая решает некоторую задачу. Часто это выполняется с использованием обучающих данных и индуктивного вывода. ГП очень близко к машинному обучению и поэтому в качестве фитнесс-функции достаточно часто выступают функции ошибки (рассогласования, невязки в различных метриках). Следует отметить, что ГП работает с генетическим материалом переменной длины, что требует нестандартной формы представления генома и соответствующих генетических операторов [3].
6.1. Функциональное и терминальное множество
Программы составляются из переменных, констант и функций, которые связаны некоторыми синтаксическими правилами. Поэтому необходимо определить терминальное множество, содержащее константы и переменные, и функциональное множество, которое состоит, прежде всего, из операторов и необходимых элементарных функций (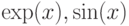 и т.п.). Следует отметить, что терминалы и функции играют различную роль. Терминалы обеспечивают входные значения в систему (программу), в то время как функции используются при обработке значений внутри системы. Термины "функции" и "терминалы" взяты из древовидного, наиболее часто применяемого, представления программ, которое широко используется в теории формальных языков и грамматик. Терминалы и функции соответствуют узлам древовидных (или графоподобных) структур.
и т.п.). Следует отметить, что терминалы и функции играют различную роль. Терминалы обеспечивают входные значения в систему (программу), в то время как функции используются при обработке значений внутри системы. Термины "функции" и "терминалы" взяты из древовидного, наиболее часто применяемого, представления программ, которое широко используется в теории формальных языков и грамматик. Терминалы и функции соответствуют узлам древовидных (или графоподобных) структур.
6.1.1. Терминальное множество
Терминальное множество включает в себя: 1) внешние входы в программу; 2) используемые в программе константы; 3) функции, которые не имеют аргументов. Слово "терминал" используется, так как перечисленные выше объекты соответствуют терминальным (конечным, висячим) вершинам в древовидных структурах и соответствуют терминалам в формальных грамматиках. Терминал дает некоторое (численное) значение, не подвергаясь никаким входным значениям. У него нет входных аргументов, и он имеет нулевую "арность".
Следует отметить тесную связь внешних входов с обучающими выборками, которые часто используются в ГП. При этом каждая переменная (признак, фактор и т.п.) обучающей выборки соответствует своему терминалу. В этом смысле ГП отличается от других методов машинного обучения. Здесь переменная выборки не привязана прямо к входным данным – связь производится через терминалы. При необходимости терминал можно связать с другой внешней переменной.
Терминальное множество включает в себя также константы. В классическом ГП, основанном на древовидном представлении, множество числовых констант выбирается для всей популяции и не меняется в процессе эволюции. Но в линейном ГП (использующем линейное представление программы) случайно генерированные (обычно из заданного диапазона) константы могут мутировать при поиске решения.
6.1.2. Функциональное множество
Функциональное множество состоит из операторов (взятых у языков программирования) и различных функций. Оно может быть достаточно широким и включать типовые конструкции различных языков программирования, такие как:
- булевы функции И, ИЛИ, НЕ и т.п.;
- арифметические функции сложения, вычитания, умножения, деления;
- трансцендентные функции (тригонометрические, логарифмические);
- функции присваивания значения переменным (
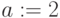 );
); - условные операторы (if then, else: case или switch операторы ветвления);
- операторы переходов (go to, jump, call- вызов функции);
- операторы цикла (while do, repeat until, for do);
- подпрограммы и функции.
С одной стороны, терминальное и функциональное множества должны быть достаточно большими для представления потенциального решения. Например, вряд ли функциональное множество из операторов сложения и вычитания может быть эффективно использовано при решении достаточно сложных проблем. С другой стороны не следует сильно без необходимости расширять функциональное множество, поскольку при этом резко возрастает пространство поиска решений. Конечно, набор функций существенно зависит от решаемой задачи. Можно начинать с простейшего множества, состоящего из арифметических операторов сложения, вычитания, умножения, деления и логических - И, ИЛИ, НЕ, ИСКЛЮЧАЮЩЕЕ ИЛИ.
Это также относится к константам. Во многих реализациях используется 256 узлов для представления функций и терминалов. Например, 56 используются для кодирования функций и 200 для констант. Важным свойством функционального множества является его замкнутость относительно принимаемых значений. То есть каждая функция должна принимать значения, которые могут принимать ее аргументы. Самым известным контрпримером является обычное деление, в котором второй аргумент (делитель) не может принимать нулевое значение. В этом случае может быть аварийный останов. Поэтому иногда используют "защищенное" деление, которое обрабатывает указанную ситуацию, возвращая в этом случае, например, некоторое большое число или нуль. Желательно, чтобы все функции (корень квадратный, логарифм и т.п.) имели подобную "защиту".
