Генетическое программирование
6.9. Символьная регрессия
Этот раздел является одним из важнейших приложений ГП. Данный термин подчеркивает то, что здесь объектом поиска является символьное описание модели, в отличие от множества коэффициентов в стандартных методах. Этот подход существенно отличается от других методов регрессии и использования нейросетей прямого распространения, где структура (и сложность) модели предполагается известной и фактически необходимо найти только ее коэффициенты. В случае символьной регрессии вид и сложность функции заранее неизвестны и могут изменяться в процессе поиска.
Задача регрессии может быть определена на основе множества значений входных независимых переменных  и зависимой выходной переменной
и зависимой выходной переменной  . Целью поиска является аппроксимация
. Целью поиска является аппроксимация  с помощью переменных
с помощью переменных  и коэффициентов
и коэффициентов  следующим образом
следующим образом 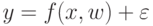 , где
, где  представляет шум (ошибку).
представляет шум (ошибку).
В стандартних методах регресии вид функции  предполагается известным, например, в линейной регресии -
предполагается известным, например, в линейной регресии - 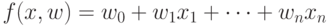 . Здесь коэффициенты
. Здесь коэффициенты 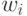 обычно находятся методом наименьших квадратов. В нелинейных методах, например с использованием нейронных сетей прямого распространения, функция имеет вид
обычно находятся методом наименьших квадратов. В нелинейных методах, например с использованием нейронных сетей прямого распространения, функция имеет вид  . Здесь коэффициенты
. Здесь коэффициенты 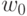 и
и 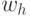 представляют синаптические веса нейронной сети выходного и скрытых слоев соответственно.
представляют синаптические веса нейронной сети выходного и скрытых слоев соответственно.
Как уже отмечалось, символьная регрессия на основе ГП не использует некоторую заранее предопределенную форму функции 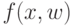 . Здесь функция
. Здесь функция 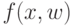 представляется древовидной структурой и строится эволюционным методом с использованием определенного функционального и терминального множеств. В качестве фитнесс-функции обычно используется квадратичная ошибка, которая оценивает качество решения и обеспечивает обратную связь при поиске решения. Для определенности обозначим функции множества, зависящие от одной переменной через
представляется древовидной структурой и строится эволюционным методом с использованием определенного функционального и терминального множеств. В качестве фитнесс-функции обычно используется квадратичная ошибка, которая оценивает качество решения и обеспечивает обратную связь при поиске решения. Для определенности обозначим функции множества, зависящие от одной переменной через 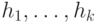 и функции от двух переменных как
и функции от двух переменных как 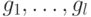 . В этой нотации функция
. В этой нотации функция 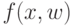 представляется в виде суперпозиции функций
представляется в виде суперпозиции функций 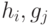 , и например, может иметь следующий вид:
, и например, может иметь следующий вид: 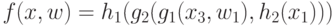 .
.
Заметим, что в символьной регрессии при поиске решения не используются численные методы, например, градиентные или стохастические.
Далее рассмотрим детально пример использования символьной регрессии из [5] для аппроксимации данных, представленных в табл.6.9. Необходимо найти функцию  , которая аппроксимирует с заданной точностью эти "экспериментальные" данные. Для решения задачи определим в соответствии с вышесказанным:
, которая аппроксимирует с заданной точностью эти "экспериментальные" данные. Для решения задачи определим в соответствии с вышесказанным:
Терминальное множество: переменная x и константы в диапазоне [-5,5];
Функциональное множество: арифметические функции 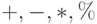 (защищенное деление).
(защищенное деление).
Koza [2] ввел следующую удобную и "прозрачную" форму для перечисления параметров, которая представлена в табл.6.10.
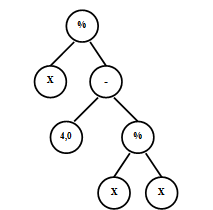
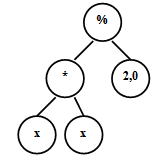
Далее приведем некоторые полученные экспериментальные данные результатов эволюции для различных запусков программ из [5]. В начальной популяции после инициализации лучшая особь представлена деревом рис.6.15, которая реализует (не минимальным образом !) функцию  .В последующих рисунках рис.6.16,рис.6.17,рис.6.18,рис.6.19,рис.6.20 представлены лучшие особи последующих поколений. Здесь в первом поколении лучшая особь реализует
.В последующих рисунках рис.6.16,рис.6.17,рис.6.18,рис.6.19,рис.6.20 представлены лучшие особи последующих поколений. Здесь в первом поколении лучшая особь реализует  .В последующих рисунках рис.6.16,рис.6.17,рис.6.18,рис.6.19,рис.6.20 представлены лучшие особи последующих поколений. Здесь в первом поколении лучшая особь реализует
.В последующих рисунках рис.6.16,рис.6.17,рис.6.18,рис.6.19,рис.6.20 представлены лучшие особи последующих поколений. Здесь в первом поколении лучшая особь реализует  и соответствующее дерево рис.6.16 сильно избыточно.
и соответствующее дерево рис.6.16 сильно избыточно.
| № | Вход 
|
Выход 
|
|---|---|---|
| 1 | 0.000 | 0.000 |
| 2 | 0.100 | 0.005 |
| 3 | 0.200 | 0.020 |
| 4 | 0.300 | 0.045 |
| 5 | 0.400 | 0.080 |
| 6 | 0.500 | 0.125 |
| 7 | 0.600 | 0.180 |
| 8 | 0.700 | 0.245 |
| 9 | 0.800 | 0.320 |
| 10 | 0.900 | 0.405 |
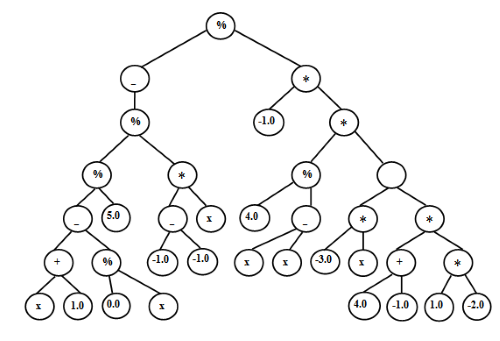
Аналогично во втором поколении лучшая особь реализует функцию 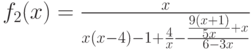 и дерево тоже сильно избыточно. Наконец в третьем поколении получена лучшая особь
и дерево тоже сильно избыточно. Наконец в третьем поколении получена лучшая особь 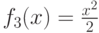 , которая дает оптимальное решение в простейшей форме.
, которая дает оптимальное решение в простейшей форме.
| Параметры | Значения |
|---|---|
| Цель: | Эволюция функции, аппроксимирующей данные Табл.6.6 |
| Терминальное множество | Переменная  , Целые от –5 до +5 , Целые от –5 до +5 |
| Функциональное множество | ADD, SUB, MUL, DIV |
| Мощность популяции: | 600 |
| Вероятн. кроссинговера: | 0.90 |
| Вероятность мутации: | 0.05 |
| Отбор родителей: | турнирный, с мощностью тура 4 |
| Максимальное число поколений: | 100 |
| Максимальная глубина после кроссинговера: | 200 |
| Максимальная глубина мутации: | 4 |
| Метод инициализации: | Растущая |
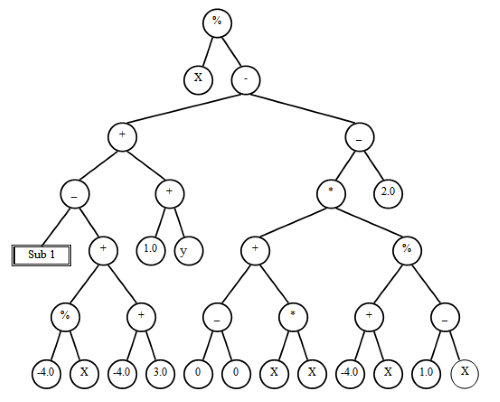
В табл.6.11 для сравнения представлены значения функций лучших особей первых поколений (0-3).Отметим, что была выполнена еще одна итерация (4-е поколение). На рис.6.19 представлена лучшая особь четвертого поколения, которая также реализует функцию 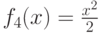 , но избыточность соответствующего дерева выросла. Конечно, для данного примера можно было использовать и классические методы регрессии, но он носит чисто иллюстративный характер.
, но избыточность соответствующего дерева выросла. Конечно, для данного примера можно было использовать и классические методы регрессии, но он носит чисто иллюстративный характер.
Интересным примером является машинный вывод третьего закона Кеплера на основе символьной регрессии. Итак, есть экспериментальные данные, которые связывают радиус и период обращения планет солнечной системы, которые представлены в табл.6.12 (в астрономических единицах).
Напомним, что согласно закону Кеплера, период обращения планеты пропорционален корню квадратному из третьей степени радиуса орбиты 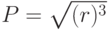 , где
, где  – радиус орбиты планеты (чаще используется формулировка
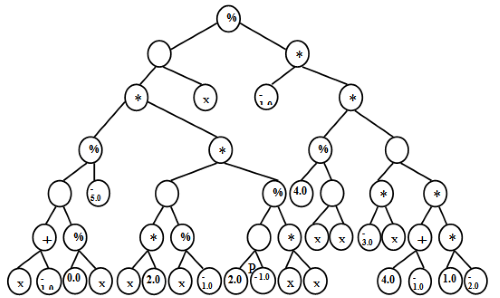
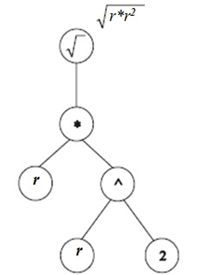
– радиус орбиты планеты (чаще используется формулировка 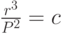 ). Для решения этой задачи с помощью символьной регрессии возможные параметры представлены в табл.6.13. На рис.6.20 представлено полученное с помощью символьной регрессии дерево, которое представляет закон Кеплера.
). Для решения этой задачи с помощью символьной регрессии возможные параметры представлены в табл.6.13. На рис.6.20 представлено полученное с помощью символьной регрессии дерево, которое представляет закон Кеплера.
Во многих работах [2,5] приведены результаты для более сложных зависимостей, но они требуют для представления результатов большого объема.
| № |  |
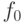 |
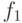 |
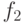 |
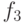 |
|---|---|---|---|---|---|
| 1 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 2 | 0.005000 | 0.033333 | 0.017544 | 0.002375 | 0.005000 |
| 3 | 0.020000 | 0.066667 | 0.037037 | 0.009863 | 0.020000 |
| 4 | 0.045000 | 0.100000 | 0.058824 | 0.023416 | 0.045000 |
| 5 | 0.080000 | 0.133333 | 0.083333 | 0.044664 | 0.080000 |
| 6 | 0.125000 | 0.166667 | 0.111111 | 0.076207 | 0.125000 |
| 7 | 0.180000 | 0.200000 | 0.142857 | 0.1222140 | 0.180000 |
| 8 | 0.245000 | 0.233333 | 0.179487 | 0.188952 | 0.245000 |
| 9 | 0.320000 | 0.266667 | 0.222222 | 0.287024 | 0.320000 |
| 10 | 0.405000 | 0.300000 | 0.272727 | 0.432966 | 0.405000 |
| Планета | Радиус - 
|
Период - 
|
|---|---|---|
| Меркурий | 0,387 | 0,24 |
| Венера | 0,723 | 0,62 |
| Земля | 1,000 | 1,000 |
| Марс | 1,524 | 1,88 |
| Юпитер | 5,203 | 11,86 |
| Сатурн | 9,569 | 29,46 |
| Уран | 19,309 | 84,01 |
| Нептун | 30,284 | 164,79 |
| Плутон | 39,781 | 247,69 |
Следует отметить, что мощность популяций используемых в ГП на порядок выше, чем в классических ГА, а число поколений, как правило, меньше. Применение ГП в качестве символьной регрессии является важным для многих технических задач (например, в гидро- и аэродинамике), но далеко не единственным.
Как показано выше, символьная регрессия может использоваться для получения эмпирических зависимостей на основе экспериментальных данных. Она широко применяется в эконометрике при решении задач моделирования и прогнозирования. Кроме этого, символьная регрессия с успехом применяется в символьных вычислениях, включая символьное дифференцирование и интегрирование, решение дифференциальных и интегральных уравнений в символьном виде и т.п.[2].