Роевые и муравьиные алгоритмы
11. Роевые алгоритмы
В настоящем разделе представлены методы роевого интеллекта, которые также являются популяционными, примыкают к эволюционным вычислениям и основаны на моделировании социального поведения. Изложен глобальный роевой алгоритм (РА), который основан на правилах взаимодействия частиц в рое – изменении их положения и скорости. Приведен также локальный роевой алгоритм, где коррекция поведения данной частицы зависит только от ее локального окружения. Описаны основные параметры и модификации РА и их влияние на эффективность метода. Приведено сравнение РА и ГА.
Роевые алгоритмы (РА), также как и эволюционные, используют популяцию особей – потенциальных решений проблемы и метод стохастической оптимизации, который навеян (моделирует) социальным поведением птиц или рыб в стае или насекомых в рое (рис.11.1)[1]. Аналогично эволюционным алгоритмам здесь начальная популяция потенциальных решений также генерируется случайным образом и далее ищется (суб)оптимальное решение проблемы в процессе выполнения РА. Первоначально в РА предпринята попытка моделировать поведение стаи птиц, которая обладает способностью порой внезапно и синхронно перегруппироваться и изменять направление полета при выполнении некоторой задачи. В отличие от ГА здесь не используются генетические операторы, в РА особи (называемые частицами- particle) летают в процессе поиска в гиперпространстве поиска решений и учитывают успехи своих соседей. Если одна частица видит хороший (перспективный) путь (в поисках пищи или защиты от хищников), то остальные частицы способны быстро последовать за ней, даже если они находились в другом конце роя. С другой стороны, в рое, для сохранения достаточно большого пространства поиска, должны быть частицы с долей "сумасшествия" или случайности в своем поведении (движении).
11.1. Основной роевой алгоритм
Итак, РА использует рой частиц, где каждая частица представляет потенциальное решение проблемы. Поведение частицы в гиперпространстве поиска решения все время подстраивается в соответствии со своим опытом и опытом своих соседей. Кроме этого, каждая частица помнит свою лучшую позицию с достигнутым локальным лучшим значением целевой (фитнесс-) функции и знает наилучшую позицию частиц - своих соседей, где достигнут глобальный на текущий момент оптимум. В процессе поиска частицы роя обмениваются информацией о достигнутых лучших результатах и изменяют свои позиции и скорости по определенным правилам на основе имеющейся на текущий момент информации о локальных и глобальных достижениях. При этом глобальный лучший результат известен всем частицам и немедленно корректируется в том случае, когда некоторая частица роя находит лучшую позицию с результатом, превосходящим текущий глобальный оптимум. Каждая частица сохраняет значения координат своей траектории с соответствующими лучшими значениями целевой функции, которые обозначим  , которая отражает когнитивную компоненту. Аналогично значение глобального оптимума, достигнутого частицами роя, будем обозначать
, которая отражает когнитивную компоненту. Аналогично значение глобального оптимума, достигнутого частицами роя, будем обозначать  , которое отражает социальную компоненту. Таким образом, каждая частица роя подчиняется достаточно простым правилам поведения (изложенным ниже формально), которые учитывают локальный успех каждой особи и глобальный оптимум всех особей (или некоторого множества соседей) роя.
, которое отражает социальную компоненту. Таким образом, каждая частица роя подчиняется достаточно простым правилам поведения (изложенным ниже формально), которые учитывают локальный успех каждой особи и глобальный оптимум всех особей (или некоторого множества соседей) роя.
Каждая  -я частица характеризуется в момент времени
-я частица характеризуется в момент времени  своей позицией
своей позицией 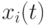 в гиперпространстве и скоростью движения
в гиперпространстве и скоростью движения 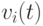 . Позиция частицы изменяется в соответствии со следующей формулой:
. Позиция частицы изменяется в соответствии со следующей формулой:
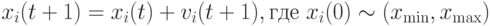 |
( 11.1) |
Вектор скорости 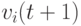 управляет процессом поиска решения и его компоненты определяются с учетом когнитивной и социальной составляющей следующим образом:
управляет процессом поиска решения и его компоненты определяются с учетом когнитивной и социальной составляющей следующим образом:
![v_{ij}(t+1)=v_{ij}(t)+c_1r_{1j}(t)[y_{ij}(t)-x_{ij}(t)]+c_2r_{2j}(t)[\hat y_{j}(t)-x_{ij}(t)]](/sites/default/files/tex_cache/2b5a908f527783bf0b8a2137d5158f34.png) |
( 11.2) |
Здесь 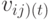 -
-  -ая компонента скорости
-ая компонента скорости 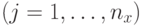
 -ой частицы в момент времени
-ой частицы в момент времени  ,
, 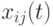 -
-  -я координата позиции
-я координата позиции  -й частицы,
-й частицы, 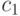 и
и 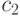 – положительные коэффициенты ускорения (часто полагаемые 2), регулирующие вклад когнитивной и социальной компонент,
– положительные коэффициенты ускорения (часто полагаемые 2), регулирующие вклад когнитивной и социальной компонент, 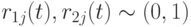 - случайные числа из диапазона [0,1], которые генерируются в соответствии с нормальным распределением и вносят элемент случайности в процесс поиска. Кроме этого
- случайные числа из диапазона [0,1], которые генерируются в соответствии с нормальным распределением и вносят элемент случайности в процесс поиска. Кроме этого  - персональная лучшая позиция по
- персональная лучшая позиция по  -й координате
-й координате  -ой частицы, а
-ой частицы, а 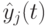 –лучшая глобальная позиция роя, где целевая функция имеет экстремальное значение.
–лучшая глобальная позиция роя, где целевая функция имеет экстремальное значение.
При решении задач минимизации персональная лучшая позиция в следующий момент времени 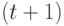 определяется следующим образом:
определяется следующим образом:
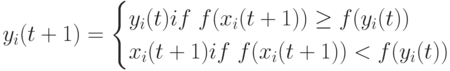 |
( 11.3) |
где  - фитнесс-функция. Как и в эволюционных алгоритмах фитнесс-функция измеряет близость текущего решения к оптимуму.
- фитнесс-функция. Как и в эволюционных алгоритмах фитнесс-функция измеряет близость текущего решения к оптимуму.
Глобальная лучшая позиция 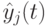 в момент
в момент  определяется в соответствии с
определяется в соответствии с
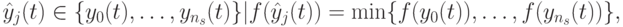 |
( 11.4) |
где 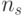 – общее число частиц в рое.
– общее число частиц в рое.
В процессе поиска решения описанные действия выполняются для каждой частицы роя. Укрупненный основной роевой алгоритм представлен ниже.
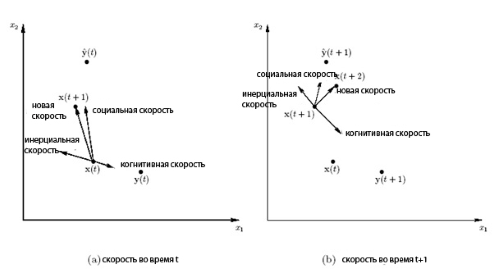
Рассмотрим влияние различных составляющих при вычислении скорости частицы в соответствии с (11.2). Первое слагаемое в (11.2) 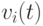 сохраняет предыдущее направление скорости
сохраняет предыдущее направление скорости  -й частицы и может рассматриваться как момент, который препятствует резкому изменению направления скорости и выступает в роли инерционной компоненты. Когнитивная компонента
-й частицы и может рассматриваться как момент, который препятствует резкому изменению направления скорости и выступает в роли инерционной компоненты. Когнитивная компонента  определяет характеристики частицы относительно ее предистории, которая хранит лучшую позицию данной частицы. Эффект этого слагаемого в том, что оно пытается вернуть частицу назад в лучшую достигнутую позицию. Третье слагаемое
определяет характеристики частицы относительно ее предистории, которая хранит лучшую позицию данной частицы. Эффект этого слагаемого в том, что оно пытается вернуть частицу назад в лучшую достигнутую позицию. Третье слагаемое 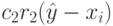 определяет социальную компоненту, которая характеризует частицу относительно своих соседей. Эффект социальной компоненты в том, что она пытается направить каждую частицу в сторону достигнутого роем (или его некоторым ближайшим окружением) глобального оптимума.
определяет социальную компоненту, которая характеризует частицу относительно своих соседей. Эффект социальной компоненты в том, что она пытается направить каждую частицу в сторону достигнутого роем (или его некоторым ближайшим окружением) глобального оптимума.
Графически это наглядно иллюстрируется для двумерного случая, как это показано на рис.11.2.
Представленный основной роевой алгоритм часто называют глобальным РА (Global Best PSO), поскольку здесь при коррекции скорости частицы используется информация о положении достигнутого глобального оптимума, которая определяется на основании информации, передаваемой всеми частицами роя. В противоположность этому подходу иногда используется локальный РА, где при коррекции скорости частицы используется информация, передаваемая только в каком-то смысле ближайшими соседними частицами роя.