Генетические алгоритмы многокритериальной оптимизации
Оптимизация по нескольким критериям требует применения специальных методов, которые существенно отличаются от стандартной техники, ориентированной на оптимизацию одной функции.
Без потери общности задачу многокритериальной оптимизации можно сформулировать следующим образом:
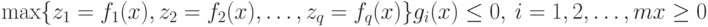
Здесь пространство поиска решений определяется следующим образом
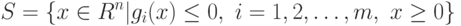
В случае многокритериальной оптимизации иногда используется графическая интерпретация как пространстве поиска решений 
, так и пространстве критериев
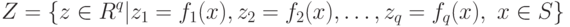
где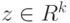 
- вектор значений 
целевых функций. Другими словами 
является множеством образов в .
5.1. Концепция доминирования Парето
Следует отметить, что многокритериальные задачи принципиально отличаются от однокритериальных. В последнем случае мы пытаемся найти решение, которое лучше всех остальных решений. В случае многокритериальной оптимизации необязательно существует решение, которое является лучшим относительно всех критериев вследствие возможных конфликтов. Решение может быть лучшим относительно одного критерия и худшим относительно других критериев.
Поэтому при многокритериальной оптимизации выполняется поиск не одной особи, а множество хромосом, оптимальных в смысле Парето [1,2,3]. Обычно пользователь имеет возможность выбирать оптимальное решение из этого множества.
Для этих целей удобно классифицировать потенциальные решения многокритериальной проблемы на доминируемые и недоминируемые решения. Решение 
называется доминируемым, если существует решение 
, не хуже чем по всем критериям, то есть для всех оптимизируемых функций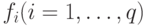 
:
для всех 
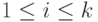при максимизации функции 
и
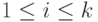для всех при минимизации функции .
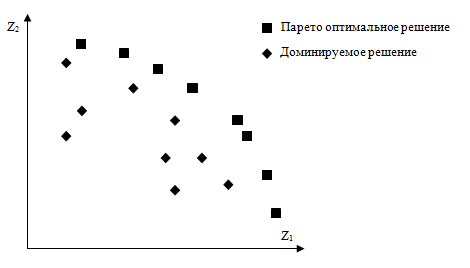
Если решение не доминируемо никаким другим решением, то оно называется недоминируемым или оптимальным в смысле Парето. Концепция Парето оптимальных решений представлена на рис.5.1, где в пространстве критериев квадратики соответствуют Парето оптимальным решениям, а ромбики – неоптимальным. При этом точка в пространстве поиска решений является действенной (эффективной), если и только если ее образ в является не доминируемым.
Присущие ГА свойства способствуют их эффективному применению при решении задач многокритериальной оптимизации, поскольку ГА основаны на использовании множества потенциальных решений - популяции и глобальном поиске в нескольких направлениях. Напомним, что ГА не предъявляют никаких требований к виду целевых функций и ограничениям.
Пусть 
и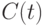 
- родители и потомки текущей популяции 
. Тогда общая структура многокритериального ГА может быть представлена следующим образом:
Фактически ГА относится к методам мета-стратегии. При применении ГА для решения конкретной задачи необходимо выбрать или разработать основные компоненты, такие как метод кодирования потенциального решения, генетические операторы кроссинговера и мутации, метод отбора родителей, построить фитнесс-функцию, позволяющую оценивать потенциальные решения и т.д.
Поскольку многокритериальная оптимизация является естественным развитием обычной численной или комбинаторной оптимизации, то многие разработанные методы были распространены на этот более общий случай. При использовании ГА для многокритериальной оптимизации центральным вопросом является построение фитнесс-функции. За последние десятилетия, следуя [2], разработано несколько подходов, которые можно разделить на представленные ниже три поколения:
- Поколение 1. Векторная оценка (vector evaluated -veGA) [5].
- Поколение 2. Ранжирование по Парето + Разнообразие:Многокритериальный ГА (multiobjective GA - moGA) [6].
- Поколение 3. Взвешенная сумма + Элитизм:Случайный взвешенный ГА (rwGA) [7]; Адаптивный взвешенный ГА (awGA)[8]; Недоминируемый ГА на основе сортировки (nsGA) [9]; Интерактивный ГА с адаптивными весами (i-awGA) [10].
Далее мы рассмотрим эти методы более подробно.