Генетические алгоритмы многокритериальной оптимизации
5.3. Ранжирование по Парето
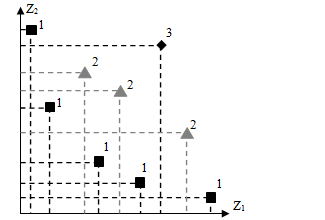
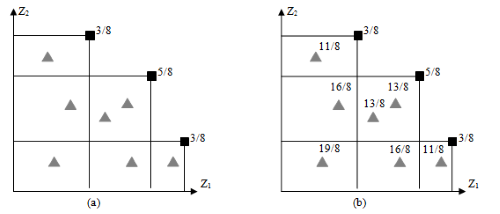
Метод ранжирования по Парето с применением ГА впервые был предложен Голдбергом [2]. Его суть в следующем: сначала присваивается ранг 1 всем недоминируемым особям, которые удаляются из дальнейшего рассмотрения. Далее среди оставшихся особей находятся недоминируемые, которым присваивается ранг 2. Этот процесс продолжается до тех пор, пока не ранжируется вся популяция. Пример представлен на рис.5.5 для простого случая минимизации относительно двух целевых функций.
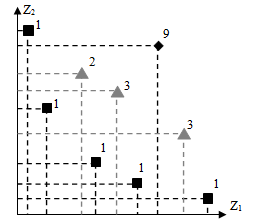
Этот подход получил развитие в последующих работах, например, в [6] предложен метод moGA, где ранг особи соответствует числу особей в текущей популяции, над которыми она доминирует. В этом случае всем недоминируемым особям присваивается ранг 1, а остальным особям присваивается ранг так, как указано выше. На рис.5.6 приведен иллюстративный пример данного метода.
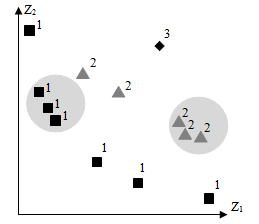
Кроме этого, ранжирование применяется в недоминируемом ГА сортировки [7] nsGA (non dominated sorting genetic algorithm). В этом методе недоминируемым решениям, составляющим фронт, присваивается фиктивные значения фитнесс-функции. Такие решения разделяются согласно этим значениям (производится разделение по фенотипу по векторам решений) и игнорируются в дальнейшем процессе классификации. В конце процедуры фиктивным значениям присваиваются значения, меньшие чем самое малое разделенное значение фитнесс-функции в текущем недоминируемом фронте.
Далее выделяется следующий фронт, и процедура повторяется до тех пор, пока все особи популяции не классифицируются. На рис.5.7 представлен пример для этого метода.
5.4. Метод взвешенной функции
Этот подход является одним из самых популярных и естественным развитием классических методов оптимизации, где новая "общая" целевая функция строится из отдельных целевых функций в виде взвешенной суммы.
![F(x)=\sum_{i=1}^k w_i f_i(x),\text{ где веса }w_i\in [0,1]\text{ и }\sum_{i=1}^k w_i=1.](/sites/default/files/tex_cache/036893fa961b7d24a21414ba2fa2344c.png)
Здесь каждой целевой функции 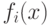 присваивается свой вес
присваивается свой вес 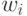 и задача сводится к скалярному случаю. При этом различные веса
и задача сводится к скалярному случаю. При этом различные веса 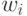 дают разные решения в смысле Парето.
дают разные решения в смысле Парето.
5.4.1. Генетический алгоритм со случайными весами
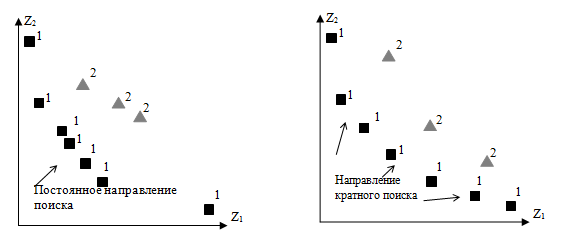
В сочетании с ГА данный поход (random-weight genetic algorithm ) rwGA впервые использован [2] для получения переменного направления поиска фронта Парето. Обычно используется два вида поиска в пространстве целей (критериев): 1) постоянное направление поиска; 2) кратное направление поиска, которые схематически показаны на рис.5.8.
При фиксированных весах в данном подходе ГА отражает тенденцию постоянного направления поиска, в то время как использование случайных весов в ГА отражает тенденцию переменного направления поиска, более приспособленной для поиска фронта решений. В rwGA каждой цели 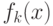 присваивается вес
присваивается вес  , где
, где 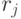 –случайные положительные числа из отрезка [0,1] и
–случайные положительные числа из отрезка [0,1] и  – число целевых функций. Скалярное значение фитнесс-функции вычисляется путем суммирования взвешенных значений целевых функций. Для паралельного поиска кратных решений веса не фиксируются, что дает возможность ГА искать весь фронт по всем направлениям. Укрупненный алгоритм представлен ниже в виде псевдокода.
– число целевых функций. Скалярное значение фитнесс-функции вычисляется путем суммирования взвешенных значений целевых функций. Для паралельного поиска кратных решений веса не фиксируются, что дает возможность ГА искать весь фронт по всем направлениям. Укрупненный алгоритм представлен ниже в виде псевдокода.
5.4.2. Эволюционный алгоритм на основе "силы" Парето
В [7] предложен "Strength Pareto Evolutionary Algorithm"(spEA), в котором удачно сочетаются некоторые черты многокритериальных ГА, рассмотренных ранее. Здесь вычисление значений фитнесс-функции выполняется в два этапа. Во-первых, ранжируются особи во внешнем недоминируемом множестве 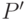 популяции. Каждому решению
популяции. Каждому решению 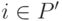 присваивается вещественное значение
присваивается вещественное значение ![s\in [0,1]](/sites/default/files/tex_cache/35a8edea94032c30d8fcc7bc7cc9c511.png) , называемое "силой", которое пропорционально числу особей
, называемое "силой", которое пропорционально числу особей 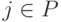 популяции для которых
популяции для которых 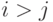 . Обозначим через
. Обозначим через  число особей в
число особей в  , которые покрываются
, которые покрываются  , и
, и  - мощность популяции. В этих обозначениях "сила"
- мощность популяции. В этих обозначениях "сила"  определяется следующим образом:
определяется следующим образом: 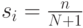 . Тогда значение фитнесс-функции
. Тогда значение фитнесс-функции  для
для  -ой цели равна ее "силе" -
-ой цели равна ее "силе" -  . Таким образом оцениваются особи популяции
. Таким образом оцениваются особи популяции  . На этой основе значение фитнесс-функции особи
. На этой основе значение фитнесс-функции особи 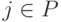 вычисляется путем суммирования "сил" всех внешних недоминируемых решений
вычисляется путем суммирования "сил" всех внешних недоминируемых решений 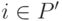 , которые покрывают
, которые покрывают  . Тогда значение фитнесс-функции
. Тогда значение фитнесс-функции
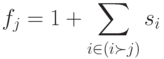
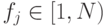 . На рис.5.9 представлен иллюстративный пример для случая максимизации с двумя целями для этого метода (spEA). Укрупненный алгоритм в виде псевдокода дан ниже.
. На рис.5.9 представлен иллюстративный пример для случая максимизации с двумя целями для этого метода (spEA). Укрупненный алгоритм в виде псевдокода дан ниже.