Муравьиные алгоритмы

12.4 Система муравьиных колоний

Дальнейшее развитие подход, разработанный в МС, получил в методе, который по современной классификации относится к "системе муравьиных колоний" (СМК) (ant colony system – ACS[7]). По сравнению с предыдущим данный метод отличается по четырем аспектам: 1) используется другое правило перехода ; 2) применяется другое правило изменения концентрации феромона; 3) вводится локальная коррекция феромона; 4) используются списки кандидатов, которые отдают предпочтение некоторым вершинам. Далее мы рассмотрим реализацию этих модификаций.

В данном методе используется правило перехода, которое можно назвать "псевдослучайно-пропорциональное", где -й муравей, находясь в вершине , выбирает очередную вершину следующим образом:

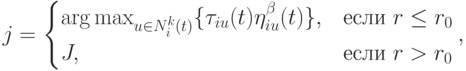( 12.17)

где 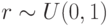, и определяется пользователем и следующий узел 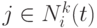выбирается случайным образом с вероятностью

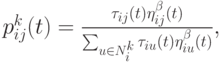( 12.18)

где 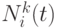множество доступных для посещения вершин. Это правило перехода отдает предпочтение коротким путям с большой концентрацией феромона. Параметр 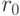используется для регулирования баланса между эксплуатацией и расширением пространства поиска решений: при алгоритм эксплуатирует пространство, выбирая лучший путь; в случае 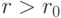алгоритм расширяет пространство поиска. Отметим, что это правило совпадает с правилом перехода МС при 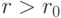. Кроме этого, фактически в правиле коэффициент 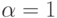(не присутствует в (12.18)). В отличие от МС здесь концентрацию феромона разрешается изменять только лучшим (в глобальном смысле) муравьям, которые построили кратчайший путь 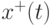, в соответствии со следующим правилом

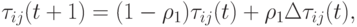( 12.19)

где

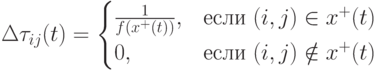( 12.20)

и 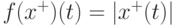в случае построения кратчайшего пути.

Использование в СМК "глобальных" правил способствует более направленному поиску, заставляя муравьев двигаться в сторону найденных лучших решений. Эта стратегия отдает предпочтение эксплуатации пространства поиска и применяется после того как решение построено.

В [7] реализовано два метода выбора пути :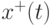

1. лучшего на итерации, где 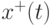представляет лучший путь, найденный за текущую итерацию, который обозначается ;
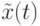2. глобально лучшего, где 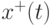представляет лучший путь, найденный с первой по текущую итерацию, который обозначается .

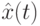Испарение феромона в СМК тоже происходит по сравнению с МС по другим правилам. Согласно (12.19) для малых значений текущая концентрация на дугах происходит медленно и влияние построенного лучшего пути ослабляется. С другой стороны, для больших значений отложенный феромон испаряется быстро и влияние построенного лучшего пути усиливается. Это способствует расширению пространству поиска. Иногда значение позволяют изменяться в процессе поиска решения: на начальной стадии используются большие значения, а на конечной – малые.

В дополнение к глобальному изменению в СМК применяется локальная коррекция концентрации феромона в соответствии со следующим правилом:

( 12.21)

где и 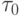- малая положительная константа. Эксперименты при решении задачи коммивояжера показали [7], что значение 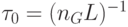дает хорошие результаты, где 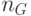- число узлов в графе и – длина тура, построенного с применением жадной эвристики.

Отметим, что в СМК также переопределяется 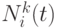- множество доступных для посещения вершин, которое содержит списки вершин-кандидатов для посещения. Пусть 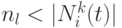означает число узлов в списке кандидатов. Ближайшие (по расстоянию или стоимости) узлов к узлу включаются в список кандидатов согласно произведенному ранжированию. При выборе следующего узла выбирается лучший из списка кандидатов. Если список кандидатов пуст, то узел выбирается из остатка 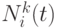. В этом случае выбор может быть сделан на основе уравнения (12.18) или же взят ближайший узел 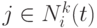. В целом алгоритм СМК представлен псевдокодом А12.4 [4].