Муравьиные алгоритмы
12.11. Параметры муравьиных алгоритмов
Эффективность МА зависит от ряда управляющих параметров, к которым относятся: 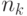 - число искусственных муравьев;
- число искусственных муравьев; 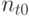 - максимальное число итераций,
- максимальное число итераций, 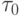 - начальная концентрация феромона,
- начальная концентрация феромона, 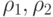 - устойчивость феромона(для ACS),
- устойчивость феромона(для ACS),  - интенсификация феромона (для ACS
- интенсификация феромона (для ACS 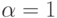 ),
),  - интенсификация эвристики. Далее мы рассмотрим эти параметры.
- интенсификация эвристики. Далее мы рассмотрим эти параметры.
Число муравьев 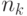 существенно влияет на характеристики МА – очевидно большое число
существенно влияет на характеристики МА – очевидно большое число 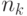 ведет к большей вычислительной сложности. Чем больше муравьев используется, тем больше путей строится и откладывается больше феромона. Например, вычислительная сложность МС оценивается
ведет к большей вычислительной сложности. Чем больше муравьев используется, тем больше путей строится и откладывается больше феромона. Например, вычислительная сложность МС оценивается 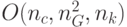 , где
, где 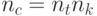 - общее число циклов,
- общее число циклов, 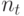 - число итераций,
- число итераций, 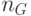 - число узлов в решениях (в предположении, что все решения имеют одинаковое число узлов).
- число узлов в решениях (в предположении, что все решения имеют одинаковое число узлов).
Успешное применение МА обусловлено, прежде всего, совместным поведением множества муравьев. Благодаря откладываемому феромону, муравьи передают полученный опыт и знания. Чем меньше используется муравьев, тем слабее способность алгоритма к исследованию и следовательно меньше информации о пространстве поиска доступно другим муравьям. Малое число муравьев может вызвать преждевременную стагнацию или нахождение субоптимальных решений. Экспериментально показано, что при решении задачи коммивояжера число муравьев, соизмеримое с числом узлов графа 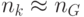 , дает хорошие результаты. Известны и более строгие оценки
, дает хорошие результаты. Известны и более строгие оценки 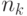 [6], в которых вычисляется оптимальное число муравьев
[6], в которых вычисляется оптимальное число муравьев
 |
( 12.38) |
где 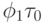 - средняя концентрация феромона на дугах лучшего пути перед глобальной коррекцией и
- средняя концентрация феромона на дугах лучшего пути перед глобальной коррекцией и 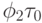 - концентрация после этой коррекции. К сожалению, оптимальные значения
- концентрация после этой коррекции. К сожалению, оптимальные значения 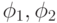 неизвестны. Экспериментальные исследования для задачи коммивояжера дают оптимальное соотношение
неизвестны. Экспериментальные исследования для задачи коммивояжера дают оптимальное соотношение 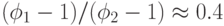 , из которого следует
, из которого следует 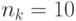 [8]. Следует подчеркнуть, что эти оценки получены только для определенного алгоритма, и в общем случае оптимальные значения
[8]. Следует подчеркнуть, что эти оценки получены только для определенного алгоритма, и в общем случае оптимальные значения 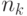 могут быть различными для разных задач.
могут быть различными для разных задач.
Максимальное число итераций 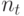 играет важную роль для поиска качественных решений. При малом числе
играет важную роль для поиска качественных решений. При малом числе 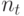 муравьям может не хватить времени для построения оптимального пути. С другой стороны, если
муравьям может не хватить времени для построения оптимального пути. С другой стороны, если 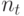 слишком велико, будут произведены лишние вычисления.
слишком велико, будут произведены лишние вычисления.
Значения начальной концентрации 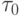 также влияют на характеристики МА. При начальной инициализации дугам обычно присваивается либо малое постоянное положительное значение
также влияют на характеристики МА. При начальной инициализации дугам обычно присваивается либо малое постоянное положительное значение 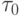 , либо малое случайное значение их диапазона
, либо малое случайное значение их диапазона ![[0,\tau_0]](/sites/default/files/tex_cache/15735dad5cb565088c57e99565818806.png) . Большое значение
. Большое значение 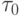 в случае случайного выбора может давать большие отличия в начальной концентрации, что может привести к начальному выбору неперспективного решения.
в случае случайного выбора может давать большие отличия в начальной концентрации, что может привести к начальному выбору неперспективного решения.
В общем случае при решении некоторой проблемы с использованием МА желательно провести экспериментальные исследования с целью оптимизации управляющих параметров.
