Муравьиные алгоритмы
12.12 Решение задач в динамической среде
При решении задач в динамической среде пространство поиска решений может изменяться. Найденное оптимальное (хорошее) решение через некоторое время вследствие изменений среды может стать неоптимальным (и даже плохим). При решении таких задач используются специальные приемы, которые помогают отслеживать изменяющуюся среду и строить оптимальные решения. МА допускают простые модификации, которые позволяет достаточно эффективно решать этот класс оптимизационных задач.
Например, при определении вероятности перехода в системе муравьиных колоний (ACS) согласно (12.18) выбор малых значений 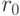 и увеличение
и увеличение  усиливают способности алгоритма к расширению пространства поиска, что необходимо при решении подобных задач. Это больше способствует выбору случайных решений, где новая измененная эвристическая информация учитывает изменяющееся окружение.
усиливают способности алгоритма к расширению пространства поиска, что необходимо при решении подобных задач. Это больше способствует выбору случайных решений, где новая измененная эвристическая информация учитывает изменяющееся окружение.
Альтернативой этому является использование корректирующего правила, где изменяются только дуги, образующие часть решения, включая испарение феромона аналогично локальному правилу всистеме муравьиных колоний (ACS). Через некоторое время концентрация феромона на часто используемых дугах уменьшается и они становятся менее предпочтительными.
Часто применяется очень простая стратегия реинициализации феромона после обнаружения изменения среды, но с сохранением ссылки на предыдущее лучшее найденное решение. Если изменение среды можно локализовать, то концентрацию феромона на соседних дугах этого участка среды можно реинициализировать максимальными значениями, что будет способствовать их выбору. Если эти дуги входят в плохие решения, то их "усиление" должно быть меньше (обычно пропорционально качеству решения) и через некоторое время "предпочтительность" этих дуг уменьшится благодаря испарению.
В [15] предложено восстанавливать решение при изменении среды. Это можно сделать с помощью локальных процедур поиска для всех решений. Компоненты, подвергшиеся изменению, устраняются из решения (дуга графа удаляется из пути, а вершина-предшественник соединяется с вершиной- последователем). Вместо удаленных компонент вносятся другие дуги,неиспользованные в решении, обычно выбираемые на основе жадных алгоритмов.
При альтернативном подходе при обнаружении окружения следует изменить правила коррекции феромона так, чтобы они способствовали расширению пространства поиска. Например, в [16] в таких ситуациях изменяются как локальные, так и глобальные правила. Локальное правило коррекции изменяется следующим образом:
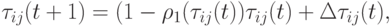 |
( 12.39) |
где 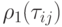 - монотонно возрастающая функция
- монотонно возрастающая функция 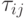 , например,
, например,
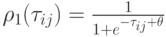 |
( 12.40) |
с 
Иногда используют изменяющиеся коэффициенты, определяющие интенсивность испарения, что ведет к тому, что на участках с большей концентраций феромон испаряется быстрее, чем на фрагментах с малой концентрацией.
Глобальная коррекция выполняется аналогично, только относительно глобально лучшего и глобально худшего решений
 |
( 12.41) |
где
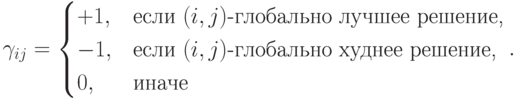 |
( 12.42) |
В работе [3] предложено три основных правила коррекции феромона при изменении среды, целью которых является поиск оптимального баланса между изменением ("сбросом") достаточно большого фрагмента информации для расширения пространства поиска и сохранения достаточной информации о полученных результатах для ускорения процесса поиска. Для каждой из этих стратегий по-разному вычисляется коэффициент "сброса" ![\gamma\in[0,1]](/sites/default/files/tex_cache/47fbb01c5d8a62d6f84cec91c7970edc.png) и используется следующее правило реинициализации феромона
и используется следующее правило реинициализации феромона
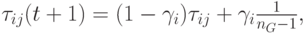 |
( 12.43) |
где 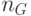 - число узлов в графе. При вычислении коэффициента сброса
- число узлов в графе. При вычислении коэффициента сброса 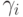 , как было сказано выше, предложены три различные стратегии:
, как было сказано выше, предложены три различные стратегии:
-
стратегия рестарта, для которой
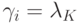
где
![\lambda_K\in[0,1]](/sites/default/files/tex_cache/27f23e5b235e1f4c16c26569f4082169.png) - параметр этой стратегии. Отметим, что данная стратегия не учитывает информацию о месте изменения среды.
- параметр этой стратегии. Отметим, что данная стратегия не учитывает информацию о месте изменения среды. -
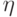 -стратегия, при которой используется эвристическая информация
-стратегия, при которой используется эвристическая информация 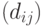

( 12.44) где

( 12.45) и

( 12.46) Здесь
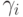 пропорционально расстоянию от изменившегося компонента и выравнивание концентрации феромона выполняется для дуг, которые инцидентны изменившийся компоненте.
пропорционально расстоянию от изменившегося компонента и выравнивание концентрации феромона выполняется для дуг, которые инцидентны изменившийся компоненте. -
 -стратегия, где выравнивание концентрации для ближних (к изменению среды) компонент больше, чем для дальних:
-стратегия, где выравнивание концентрации для ближних (к изменению среды) компонент больше, чем для дальних: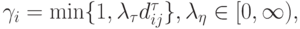
( 12.47) где

( 12.48) и
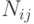 - множество всех путей от
- множество всех путей от  до
до  .
.
