Муравьиные алгоритмы
12.3.Муравьиная система
Первый муравьиный алгоритм был разработан M.Дориго[2].По современной классификации он относится к (antsystem) муравьиной системе (МС). По сравнению с простым муравьиным алгоритмом в МС улучшены характеристики за счет изменения метода вычисления вероятности выбора следующей вершины путем учета эвристической информации и ввода списка запрещенных вершин (tabulist). Конкретно, в МС вероятность перехода из  -ой вершины в
-ой вершины в  -ю вершину определяется следующим образом
-ю вершину определяется следующим образом
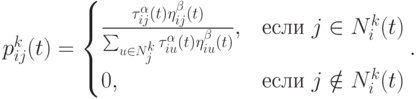 |
( 12.6) |
где: 1) 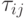 представляет апостериорную эффективность перехода из вершины
представляет апостериорную эффективность перехода из вершины  в
в  , которая определяется интенсивностью феромона для соответствующей дуги; 2)
, которая определяется интенсивностью феромона для соответствующей дуги; 2) 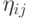 представляет априорную эффективность перехода из
представляет априорную эффективность перехода из  в
в  на основе некоторой эвристики.
на основе некоторой эвристики.
Вероятность перехода в МС, определяемая (12.6), отличается от аналога в ПМА, заданной (12.2), двумя аспектами:
- При вычислении вероятности перехода в МС предпринята попытка сбалансировать влияние интенсивности феромона
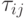 (отражающее предысторию успешных действий) и эвристической информации
(отражающее предысторию успешных действий) и эвристической информации 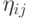 (выражающее предпочтительность некоторого выбора). Этот баланс управляет процессом эксплуатации-расширения в пространстве поиска решения. Баланс регулируется значениями коэффициентов
(выражающее предпочтительность некоторого выбора). Этот баланс управляет процессом эксплуатации-расширения в пространстве поиска решения. Баланс регулируется значениями коэффициентов  и
и  . При
. При 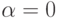 информация о концентрации феромона не используется и предыдущий опыт игнорируется. Если
информация о концентрации феромона не используется и предыдущий опыт игнорируется. Если  , то не учитывается эвристическая информация и мы имеем простой МА. Эвристическая информация о предпочтительности выбора следующей вершины можетпредставляться в различной форме и зависит от задачи. Например, для выбора кратчайшего пути можно использовать
, то не учитывается эвристическая информация и мы имеем простой МА. Эвристическая информация о предпочтительности выбора следующей вершины можетпредставляться в различной форме и зависит от задачи. Например, для выбора кратчайшего пути можно использовать 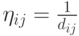 , где
, где 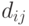 - расстояние между вершинами
- расстояние между вершинами  и
и  . Очевидно, что в этом случае предпочтительней короткая дуга, исходящая из вершины
. Очевидно, что в этом случае предпочтительней короткая дуга, исходящая из вершины  .
. - Множество
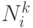 определяет множество допустимых вершин для
определяет множество допустимых вершин для  -го муравья. Это множество может включать соседние к
-го муравья. Это множество может включать соседние к  вершины, которые не посещались
вершины, которые не посещались  -м муравьем. Для этого для каждого муравья создается и отслеживается табу-список. Вершины из этого списка удаляются из
-м муравьем. Для этого для каждого муравья создается и отслеживается табу-список. Вершины из этого списка удаляются из 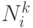 , поскольку каждая вершина может посещаться только один раз.
, поскольку каждая вершина может посещаться только один раз.
Некоторые авторы [6] вместо (12.6) в МС используют другую форму выражения для вероятности:
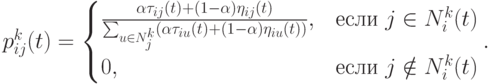
( 12.8)
Здесь параметр  определяет относительную важность концентрации феромона
определяет относительную важность концентрации феромона 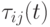 по сравнению с эвристикой
по сравнению с эвристикой 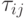 . Данный вариант МС по сравнению с предыдущим не требует задания параметра
. Данный вариант МС по сравнению с предыдущим не требует задания параметра  .
.
Испарение феромона реализуется согласно (12.5) – после построения пути каждым муравьем, концентрация феромона на каждой дуге корректируется следующим образом:
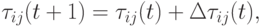 |
( 12.9) |
где
 |
( 12.10) |
и  - количество феромона, откладываемое муравьем
- количество феромона, откладываемое муравьем  на дуге
на дуге 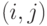 в момент времени
в момент времени  .
.
M.Дориго разработал три модификации МС, которые отличаются методом вычисления 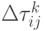 (в предположении, что решается задача минимизации):
(в предположении, что решается задача минимизации):
-
Ant-cycle AS, где
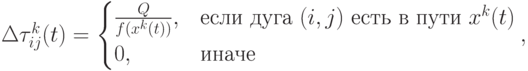
( 12.11) где
 - положительная константа. Здесь количество феромона откладывается обратно пропорционально качеству
- положительная константа. Здесь количество феромона откладывается обратно пропорционально качеству  на дугах полного пути, построенного муравьем. При этом для изменения концентрации феромона используется глобальная информация.
на дугах полного пути, построенного муравьем. При этом для изменения концентрации феромона используется глобальная информация.При решении задач максимизации в этом случае
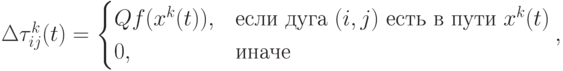
( 12.12) -
Ant-density AS, где
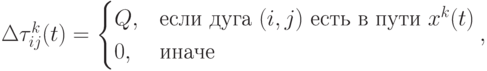
( 12.13) В этой модификации каждый муравей откладывает одинаковое количество феромона на любой дуге построенного пути. Этот подход учитывает только количество муравьев, прошедших по данной дуге
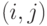 . Чем выше плотность трафика на дуге, тем более она привлекательна для окончательного решения.
. Чем выше плотность трафика на дуге, тем более она привлекательна для окончательного решения. -
Ant-quantity AS, для которой

( 12.14) В этом случае при коррекции концентрации феромона используется только локальная информация – расстояние
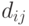 и МС предпочитает выбирать короткие дуги.
и МС предпочитает выбирать короткие дуги.
В целом МС-алгоритм представлен ниже псевдокодом A12.3[6]. Здесь на этапе инициализации размещение муравьев определяется решаемой задачей. Если целью является поиск кратчайшего пути между заданными вершинами графа, то все 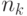 муравьев размещаются на начальной вершине. С другой стороны, если целью является построение кратчайшего гамильтонова цикла (соединяющего все вершины), то
муравьев размещаются на начальной вершине. С другой стороны, если целью является построение кратчайшего гамильтонова цикла (соединяющего все вершины), то 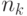 муравьев случайно размещаются на всем графе. Это расширяет пространство поиска. Инициализация феромона выполняется с помощью либо малой константы
муравьев случайно размещаются на всем графе. Это расширяет пространство поиска. Инициализация феромона выполняется с помощью либо малой константы 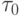 , либо небольших значений из диапазона
, либо небольших значений из диапазона ![[0,\tau_0]](/sites/default/files/tex_cache/15735dad5cb565088c57e99565818806.png) .
.
Автор МС M.Дориго[6] исследовал характеристики всех трех приведенных модификаций, прежде всего, при решении задачи коммивояжера. Версия Ant-cycle AS работала быстрее, в силу использования глобальной информации.
Кроме этого Дориго[6] ввел стратегию элитизма, где в дополнение коррекции феромона согласно (12.4) дополнительно добавляется количество феромона, пропорциональное длине лучшего пути для всех его дуг следующим образом:
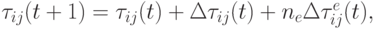 |
( 12.15) |
где
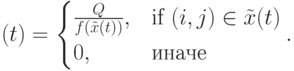 |
( 12.16) |
Здесь  – число элитных муравьев,
– число элитных муравьев, 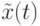 - лучшее корректное решение с
- лучшее корректное решение с  .
.

