Быстрое преобразование Фурье
Быстрое преобразование Фурье (БПФ) - умный, быстрый алгоритм вычисления ДПФ. Цель остается та же - вычислить коэффициенты Фурье:
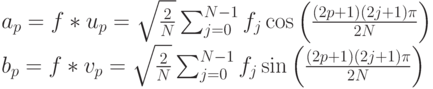
Давайте оценим сложность, задаваемую этими формулами. При определении вычислительной сложности будем учитывать число умножений, игнорируя сложения, поскольку это более легкие операции в сравнения с умножением. Мы предполагаем, что значения синусов и косинусов предварительно вычислены и хранятся в памяти. Проигнорируем множитель 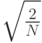 , так как можно выбрать N/2 как степень 4, тогда деление на степень 2 является простой операцией для компьютера.
, так как можно выбрать N/2 как степень 4, тогда деление на степень 2 является простой операцией для компьютера.
Вычисления каждого коэффициента Фурье, будет тогда включать N умножений, а поскольку коэффициентов тоже N, то сложность ДПФ, вычисляемого по этим формулам - 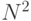 .
.
БПФ позволяет вычислить те же коэффициенты, но со сложностью 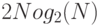 . Для вектора длины 1024 (что не является чем-то необычным при цифровой обработке сигнала) сложность прямого метода -1048576, а БПФ - 20480. БПФ - рекурсивный алгоритм. Его идея -разбить исходный вектор на два вектора половинной длины, применить рекурсивно БПФ к каждому короткому вектору, а затем комбинировать две последовательности коэффициентов Фурье, построенные для коротких векторов, в последовательность коэффициентов полного вектора.
. Для вектора длины 1024 (что не является чем-то необычным при цифровой обработке сигнала) сложность прямого метода -1048576, а БПФ - 20480. БПФ - рекурсивный алгоритм. Его идея -разбить исходный вектор на два вектора половинной длины, применить рекурсивно БПФ к каждому короткому вектору, а затем комбинировать две последовательности коэффициентов Фурье, построенные для коротких векторов, в последовательность коэффициентов полного вектора.
С этого момента будем полагать, что N - степень 2, 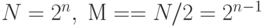
Давайте разделим вектор 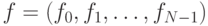 на два коротких вектора, где компоненты с четными индексами будут принадлежать одному вектору, с нечетными - другому,
на два коротких вектора, где компоненты с четными индексами будут принадлежать одному вектору, с нечетными - другому, 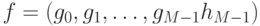 Пока что, мы только ввели новую нотацию, не производя никаких вычислений:
Пока что, мы только ввели новую нотацию, не производя никаких вычислений:
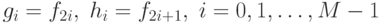
В результате созданы два вектора длины 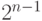 :
:
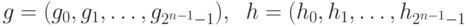
Давайте применим ДПФ к векторам g и h:
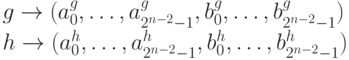
Коэффициенты Фурье для g и h соответственно имеют вид:
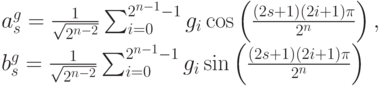
Формулы для коэффициентов 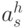 и
и 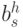 аналогичны.
аналогичны.
Теперь покажем, как можно сконструировать коэффициенты Фурье 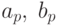 для вектора f из коэффициентов:
для вектора f из коэффициентов: 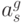 и
и 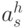 ,
,  и
и