Криптография: от Римской Империи до квантовых методов
В 1970-м году изобретение криптосистемы с открытым ключом произвело революцию в криптографии. В наши дни шифрование с открытым ключом широко используется в Интернет коммерции. Одна из целей этого курса объяснить, как квантовые вычисления могут быть использованы для взлома криптосистем с открытым ключом. Мы будем обсуждать эту тему на протяжении всего курса. В этой главе мы разберем старые методы - криптографию с секретным ключом и покажем, как квантовые методы могут сделать эти методы более эффективными.
Юлий Цезарь был первым, кто систематически применял шифрование. Он шифровал военные сообщения, используя код, который теперь называется кодом Цезаря. При записи своих сообщений каждая буква заменялась буквой, отстоящей в алфавите на 3 позиции левее. При этом алфавит рассматривался как циклический, - после последней буквы следовали начальные буквы алфавита:
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЪЭЮЯ ЭЮЯАБОГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЪ
так что текст ЮЛИЙ ЦЕЗАРЬ кодировался как ЫИЁЖ УВЕЭНЧ.
Мы можем дать математическую интерпретацию этого шифра, используя концепцию остатков. Рассмотрим все возможные остатки от деления нацело целых на некоторое фиксированное число m (для приложения к криптографии в этой главе будем полагать m = 33- длине алфавита кириллицы). Множество остатков обозначим как 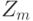 и оно содержит остатки от 0 до m - 1. Нетрудно видеть, что для вычисления остатка суммы двух целых достаточно знать остатки слагаемых, а не сами слагаемые. Это же верно и применительно к операции умножения целых.
и оно содержит остатки от 0 до m - 1. Нетрудно видеть, что для вычисления остатка суммы двух целых достаточно знать остатки слагаемых, а не сами слагаемые. Это же верно и применительно к операции умножения целых.
Давайте докажем этот простой факт. Прежде всего заметим, что два целых а и b имеют одинаковые остатки при делении на m, если разность а - b делится на m. Предположим, что мы складываем две пары целых  и
и  . Нам нужно показать, что если
. Нам нужно показать, что если 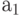 и
и  имеют одинаковые остатки и
имеют одинаковые остатки и 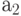 и
и 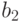 имеют одинаковые остатки, то
имеют одинаковые остатки, то  и
и  также имеют одинаковые остатки. В самом деле, рассмотрим разность:
также имеют одинаковые остатки. В самом деле, рассмотрим разность:

Оба слагаемые в правой части делятся на т, так что остаток от деления на т равен 0, откуда и следует наше утверждение.
В приведенном выводе можно полагать, что  - сумма исходных слагаемых, а
- сумма исходных слагаемых, а  - сумма их остатков. Отсюда и следует, что остаток от суммы слагаемых равен остатку от суммы остатков слагаемых.
- сумма их остатков. Отсюда и следует, что остаток от суммы слагаемых равен остатку от суммы остатков слагаемых.
Аргументация для произведения подобна:
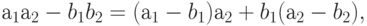
и мы приходим к аналогичному заключению.
Это позволяет нам определить сложение и умножение остатков в 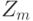 для вычисления суммы двух остатков (соответственно произведения) необходимо сложить (умножить) остатки как целые и взять остаток от результата. Для вычислений с остатками мы используем нотацию " mod m" в конце строки, чтобы указать, что равенства имеют место для остатков, а не для целых:
для вычисления суммы двух остатков (соответственно произведения) необходимо сложить (умножить) остатки как целые и взять остаток от результата. Для вычислений с остатками мы используем нотацию " mod m" в конце строки, чтобы указать, что равенства имеют место для остатков, а не для целых:
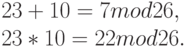
Теперь применим технику остатков к коду Цезаря, присвоив каждой букве остаток из  : А-1, Б-2, ... , Э-31, Ю-32, Я-0. Тогда шифрование делается вычитанием 3 из кода каждой буквы. При вычитании можно получить отрицательный результат Чтобы вернуться в множество
: А-1, Б-2, ... , Э-31, Ю-32, Я-0. Тогда шифрование делается вычитанием 3 из кода каждой буквы. При вычитании можно получить отрицательный результат Чтобы вернуться в множество 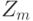 , нужно прибавить т к результату. Дешифрование выполняется прибавлением 3 к коду каждой буквы.
, нужно прибавить т к результату. Дешифрование выполняется прибавлением 3 к коду каждой буквы.
Цезарь мог использовать такой простой способ шифрования, поскольку в то время он представлял инновационную идею и его враги были необразованными. Более сложный способ шифрования - код Вигинера пришел на смену кода Цезаря. В коде Вигинера для шифрования выбирается секретное слово, представляющее ключ для шифрования и дешифрования. Для иллюстрации этого метода используем слово КУБИТ как секретное слово и зашифруем с его помощью текст: СПОСОБ ПОЛЯРИЗАЦИИ ФОТОНА
С К 19 12 31 Э П У 17 21 5 Д О Б 1б 2 18 Р С И 19 10 29 Ы О Т 1б 20 3 В Ь К 2 12 14 М П У 17 21 5 Д О Б 16 2 18 Р Л И 13 10 23 Х Я Т 0 20 20 Т Р К 18 12 30 Ъ и v 1о г1 31 э 3 Б 9 2 11 Й А И 1 10 11 Й Ц Т 24 20 11 Й И К 10 12 22 Ф И У 10 21 31 Э Ф Ь 22 г 24 Ц О И 1б 10 26 Ш Т Т 20 20 7 Ё О К 16 12 28 Ь Н У 15 21 3 13 А Б 1 2 3 13
В первом столбце таблицы сверху вниз записан кодируемый текст. В следующем столбце параллельно записан текст той же длины, что и кодируемый текст. Этот текст составлен из циклически взятого секретного слова. Код кодируемой буквы исходного текста задается суммой кода буквы и кода соответствующей буквы секретного слова. В отличие от кода Цезаря теперь у каждой буквы кодируемого текста величина сдвига не является постоянной, а определяется секретным словом. Декодирование выполняется аналогичным образом, используя вычитание кода секретной буквы.
Еще одним обобщением кода Цезаря является подстановочный шифр, где вместо сдвига в алфавите используется, например, секретная перестановка букв алфавита. Вот пример:
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЪЭЮЯ ЁЙЦУКЕНГШЩЗХЪФЫВАПРОЛДЖЭЯЧСМИТЬБЮ
Этот код может быть взломан, используя тот факт, что частота вхождения разных букв в текст существенно различается. Поэтому имея достаточно длинный зашифрованный текст можно определить какие символы встречаются наиболее часто и поставить им в соответствие часто встречающиеся буквы алфавита. В кириллице наиболее часто встречается буква О. Вот таблица, задающая частоту вхождения различных букв кириллицы в тексты:
Эта же идея использования частотного анализа может применяться для взлома шифра Вигинера. Но в этом случае потребуется применение метода " проб и ошибок", задавая при каждой попытке фиксированную длину секретного слова. Если предположить, что длина секретного слова равна 5, то из этого следует, что 1-я, 6-я, 11-я, 16-я и так далее буквы зашифрованного текста используют одну и ту же подстановку. Выделив соответствующие последовательности букв можно применить к ним частотный анализ и расшифровать текст. Если частоты последовательностей не совпадают с частотами букв, характерными для языка, то наша гипотеза о длине секретного слова не корректна и нужно сделать следующую пробу, изменив длину секретного слова.
Слабость шифра Вигинера в ограниченном размере секретного слова. Современные требования к криптографии требуют, чтобы код нельзя было взломать, даже имея большой поток зашифрованной информации.
Пусть обе стороны, посылающие закодированный текст, и получающие его для декодирования, имеют возможность доступа к общему секретному потоку случайных битов. Тогда они могут использовать этот поток для кодирования и декодирования:

