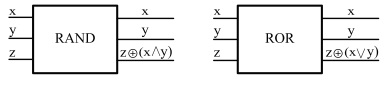Квантовые стандартные элементы и схемы
В этой лекции мы собираемся показать, как преобразовать логические схемы в квантовые схемы, реализующие классические вычисления на квантовом компьютере.
Как уже обсуждалось, квантовые вычисления должны быть обратимыми, в то время как классические элементы схемы {АND, ОR} таковыми не являются. Эта проблема решается комбинированием входных и выходных битов и созданием обратимых (реверсивных) аналогов {РАМР, ROR}, каждый из которых является функцией, принимающей на входе 3 бита, и создающей на выходе результат из трех битов: Эти элементы вычисляют 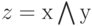
и 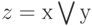 при условии, что z инициализируется нулем. Эти элементы обратимы и двойное применение элемента восстанавливает входные данные.
при условии, что z инициализируется нулем. Эти элементы обратимы и двойное применение элемента восстанавливает входные данные.
Элемент NОТ изначально обратим и совместим с квантовыми вычислениями, так что отпадает необходимость в его модификации.
Необходима еще одна операция, которую следует добавить в наш инструментарий. В классических вычислениях нетрудно вьшолнить копирование данных. Операция копирования - создание дубля - не является обратимой. Для создания квантового аналога копирования необходимо применить метод комбинирования входа и выхода к функции f (х) = х. Таким способом мы получаем элемент, который называется СNОТ: Этот элемент выполняет копирование классического бита х при условии, что бит выхода у инициализирован нулем: CNOT(х, 0) = (х, х). Имя СNОТ- сокращение названия "Сontrolled NОТ", связанного с тем, как этот элемент используется в электронике, если х = 1, то значение у меняется на противоположное, если х = 0, то у не изменяется.
Давайте покажем, что СNОТ копирует только значения классических битов, но не произвольные квантовые состояния. Посмотрите, что происходит
при применении СN0Т к суперпозиции классических состояний:

Копирование квантового состояния означало бы следующее преобразование, отличное от действия СМОТ:

Фактически, существует теорема, утверждающая, что копирование неизвестного квантового состояния невозможно.
Заметьте, что как и в выше приведенном примере, СN0Т создает запутывание. Оригинальное состояние 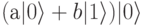 можно факторизовать, представив в виде произведения, следовательно, оно не запутанно. В то время как состояние
можно факторизовать, представив в виде произведения, следовательно, оно не запутанно. В то время как состояние 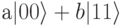 является запутанным при условии, что
является запутанным при условии, что 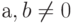 .
.
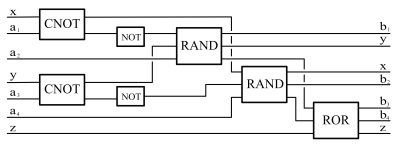
Теперь становится простым делом превратить классическую схему в квантовую схему Давайте покажем это на примере функции f (х, у) = х + у mod 2. Классическую схему, приведенную в предыдущей главе, преобразуем в квантовую схему, используя элементы RAND, RОR, NОТ, СNОТ:
Для рассматриваемой функции f (х, у) = х + у mod 2 можно построить существенно более простую квантовую схему, используя только элементы СNОТ. Цель этого упражнения в том, чтобы показать, как любую классическую схему можно транслировать в квантовую схему.
Заметьте, в квантовой схеме используются не только входные и выходные переменные, но и дополнительные переменные для хранения результатов промежуточных вычислений. Это совершенно совпадает с тем, как ведутся классические вычисления, где используется внутренняя память для хранения промежуточных результатов.
При разработке программного комплекса используются компиляторы для конвертирования кода, написанного на языке высокого уровня, в код, который может выполнять процессор. Сложные комплексы имеют модульную структуру, сразу же, когда модуль завершает работу, компилятор должен освободить память, которая была отведена дополнительным рабочим переменным. Задача по освобождению памяти называется "сборкой мусора".
Желательно и в квантовых вычислениях точно также выполнять сборку мусора. Этому есть две причины. Во-первых, нам могут понадобиться кубиты, которые были заняты хранением промежуточных результатов, а во-вторых, наши выходные биты могут стать запутанными с кубитами, хранящими дополнительные переменные, тогда все, что происходит с дополнительными кубитами, будет отражаться на битах выходных переменных.
Квантовая сборка мусора означает, что все дополнительные кубиты, имеющие значение 0 до начала вычислений, должны иметь значение 0 и в конце вычислений.
Теорема. Для любого классического вычисления существует квантовая схема, реализуемая это вычисление, с квантовой сборкой мусора.
Доказательство. Рассмотрим квантовую реализацию классической булевой функции 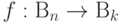 . Пространство кубитов для этой реализации разделяется на входные, выходные и дополнительные кубиты. Квантовая схема
. Пространство кубитов для этой реализации разделяется на входные, выходные и дополнительные кубиты. Квантовая схема 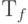 преобразует:
преобразует: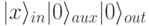 в
в 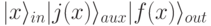 . Здесь
. Здесь  -входные кубиты,
-входные кубиты,  - дополнительные кубиты,
- дополнительные кубиты, 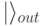 - выходные кубиты, а
- выходные кубиты, а 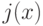 -это мусор, не представляющий интереса, созданный в процессе вычислений квантовой схемы.
-это мусор, не представляющий интереса, созданный в процессе вычислений квантовой схемы.
Для реализации квантовой сборки мусора удвоим размер выходного пространства, создав новые кубиты  с тем же числом кубитов, что имеет
с тем же числом кубитов, что имеет 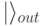 . Будем теперь рассматривать старое пространство выходных кубитов как часть пространства дополнительных кубитов. Выполнение квантовых вычислений будем теперь вести в три этапа:
. Будем теперь рассматривать старое пространство выходных кубитов как часть пространства дополнительных кубитов. Выполнение квантовых вычислений будем теперь вести в три этапа:
Этап 1. Применим трансформацию Т1:

Этап 2. Используя СN0Т, копируем 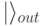 в
в  . В результате получим:
. В результате получим:

Этап З. Применяя обратную трансформацию  , получим:
, получим:

По завершении третьего этапа все дополнительные биты, включая старые выходные биты примут значение О.
Для реализации обратной трансформации  построим квантовую схему, где все квантовые элементы
построим квантовую схему, где все квантовые элементы 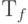 размещены в обратном порядке. Так как каждый элементарный квантовый элемент является обратным по отношению к себе, то в результате произойдет откат к состоянию, предшествующем вьшолнению
размещены в обратном порядке. Так как каждый элементарный квантовый элемент является обратным по отношению к себе, то в результате произойдет откат к состоянию, предшествующем вьшолнению 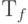 .
.
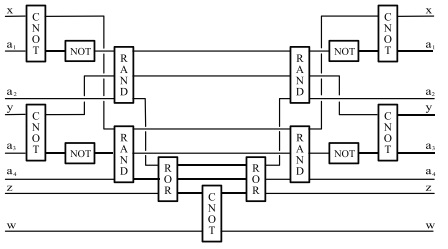
Приведем пример модифицированной квантовой схемы, вычисляющей х + у mod 2, с квантовой сборкой мусора.