Группы Ли
Группы Ли названы в честь норвежского математика Софуса Ли, который первый начал их изучать. Группы Ли - это группы симметрии, обладающие свойством непрерывности. Прототипом групп Ли является группа поворотов на сфере. Фиксируя ось вращения, можно непрерывно изменять угол поворота. Альтернативно, можно зафиксировать угол поворота и непрерывно изменять ось вращения. Можно, конечно, одновременно изменять положение оси и угол поворота.
Такого эффекта нет для группы симметрии на кубе, где симметрии не допускают непрерывной деформации. Если повернуть куб на малый угол, то он не будет самосовместимым, так что такие повороты не обеспечивают симметрию куба.
Наша цель - разобраться с группами О(n) ортогональных трансформаций. Начнем со случая ортогональных трансформаций в 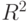 .
.
Группа О(2) - группа трансформаций круга. Ее представление во многом аналогично представлению диедральной группы - элементы О(2) принадлежат тем же типам: поворотам и отражениям.
Вспомним выражение для матриц поворота:
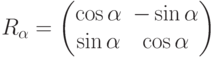
Давайте также рассмотрим отражение Т относительно оси Х:
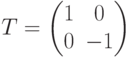
Тогда все другие отражения могут быть сконструированы как произведение Т со всеми возможными поворотами:
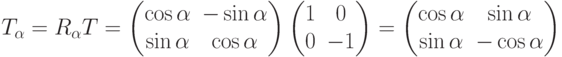
Заметьте, 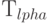 - матрица отражения, которую мы записывали в лекции 6.
- матрица отражения, которую мы записывали в лекции 6.
В итоге мы получили алгебраическое описание группы О(2).
Теорема. Группа О(2) содержит элементы 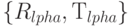 , где
, где  -угловой параметр, так что
-угловой параметр, так что 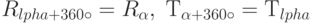 . Умножение в О(2) задается следующими соотношениями:
. Умножение в О(2) задается следующими соотношениями:
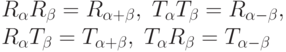
Доказательство. Так как 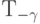 - отражение, то его обращение совпадает с самим элементом:
- отражение, то его обращение совпадает с самим элементом: 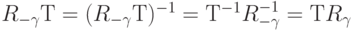 . Используя это соотношение, можно вычислить:
. Используя это соотношение, можно вычислить:
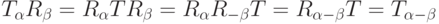
Проверка других соотношений аналогична и остается в качестве упражнений.
Оказывается, что и здесь группа О(3) состоит из элементов двух типов, один из которых - пространственные повороты (вокруг некоторых осей). Второй тип элементов в О(3) включает отражения относительно плоскости. Для более детального описания ортогональной трансформаций в трехмерном пространстве нам понадобится некоторая теорема из линейной алгебры. Доказательство этой теоремы несложно, но включает концепцию собственных значений. Так как это более продвинутая тема линейной алгебры, то мы пропустим доказательство.
Теорема. Пусть Т - ортогональная трансформация в 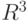 . Тогда здесь существует единичный вектор v, такой что Тv = v, либо Тv = -v.
. Тогда здесь существует единичный вектор v, такой что Тv = v, либо Тv = -v.
Пусть v - вектор из теоремы и пусть u - вектор, ортогональный v. Так как Т - ортогональная трансформация, вектора Тv, Тu ортогональны друг другу. Принимая в учет, что 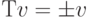 , заключаем вектор Тu ортогонален v. В результате мы видим, что плоскость, ортогональная v, инвариантна по отношению к трансформации Т, то есть Т трансформирует вектора из этой плоскости в вектора в той же плоскости. Следовательно, ограничиваясь плоскостью, ортогональной вектору v, Т является двумерной ортогональной трансформацией, либо поворотом в этой плоскости, либо отражением по отношению к линии в этой плоскости.
, заключаем вектор Тu ортогонален v. В результате мы видим, что плоскость, ортогональная v, инвариантна по отношению к трансформации Т, то есть Т трансформирует вектора из этой плоскости в вектора в той же плоскости. Следовательно, ограничиваясь плоскостью, ортогональной вектору v, Т является двумерной ортогональной трансформацией, либо поворотом в этой плоскости, либо отражением по отношению к линии в этой плоскости.
В аргументации, приводимой ниже, мы используем тот факт, что отражение плоскости имеет вектор, который трансформируется в противоположный вектор, и вектор, который трансформируется сам в себя. Первый вектор перпендикулярен линии отражения, в то время как второй вектор лежит на линии отражения.
Рассмотрим три случая:
(1) Т имеет единичный вектор v, такой что Тv = v, но не имеет единичного вектора w, такого что Tw = -w.
(2) Т имеет единичный вектор w, такой что Tw = -w, но не имеет единичного вектора v, такого что Тv = v.
(3) Т имеет оба единичных вектора v и w, такие что Тv = v и Тw = -w.
В первом случае трансформация Т должна быть поворотом на плоскости, перпендикулярной вектору v, так как Т не преобразует ни один вектор в его противоположность. Следовательно, Т - пространственный поворот вокруг оси v.
Во втором случае Т вращает плоскость, перпендикулярную w, следовательно, Т является композицией поворота плоскости и отражения относительно той же плоскости. Отражение изменяет вектор w на противоположный, поворот изменяет вектор, лежащий на линии отражения.
В случае (3) заметим, что вектора v, w должны быть перпендикулярны друг другу, так как Т сохраняет скалярное произведение: v*w=Tv*Tw=v*(-w)=-v*w, из чего следует, что v*w=0. Возьмем единичный вектор u, который перпендикулярен векторам v и w. Тогда Тu перпендикулярна Тv = v и Тw = -w, это означает, что Тu пропорционально u. Так как Т сохраняет длины, то либо Тu = u, либо Tu = -u. Мы сконструировали ортонормальный базис 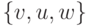 с трансформацией Т, действующей следующим образом:
с трансформацией Т, действующей следующим образом: