НОУ ИНТУИТ | Квантовые вычисления. Лекция 19: Алгоритм Шора

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 03.06.2019 | Доступ: свободный | Студентов: 491 / 71 | Длительность: 09:11:00

Темы: Программирование, Математика, Физика, Суперкомпьютерные технологии

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Ключевые слова: алгоритм, Произведение, криптосистема, RSA, Дополнение, ПО, делителем, вычисление, список, множитель, функция, выход, бит, остаток, значение, коэффициенты, вероятность, график

Настало время связать воедино все разработанные нами нити исследований и описать квантовый алгоритм Шора факторизации больших целых чисел.

Пусть р и q - два большие секретные простые числа, и N = рq их произведение. Наша цель - найти р и q при заданном N. Решение этой задачи означает, что криптосистема RSA будет взломана.

Как мы видели, мы можем определить р и q, если в дополнение к N будем знать размер группы Z_N^* - группы обратимых остатков по модулю N. Число элементов группы Z_N^* мы обозначаем как М = (р - 1) (q - 1) .

Идея определения М состоит в том, чтобы найти порядки элементов группы Z_N^* . По теореме Лагранжа порядок каждого элемента группы является делителем М, следовательно, вычисление порядков даст нам делители М.

Давайте проиллюстрируем эту идею на следующем примере. Пусть простые секретные числа - это р = 36013, q = 51199, тогда N = pq = = 1843829587. Числа р -1 и q -1 факторизуются (разлагаются на множители)следующим образом: р-1=2х2х3х3001,q-1=2х3х7х23х53. На практике факторизация неизвестна, поскольку сами простые числа р и q неизвестны. Все же для иллюстрации полезно видеть эту факторизацию, поскольку она проливает свет на порядки элементов группы Z_N^* . Порядок этой мультипликативной группы равен М = (р - 1) (q - 1) = 1843742376 = 2 х 32 х 7х 23 х 53 х 3001.

Предположим, что у нас есть способ вычисления порядков элементов этой группы. Давайте перечислим порядки элементов этой группы. Приведем список порядков нескольких элементов:

g	order of g	factorization оГ the order
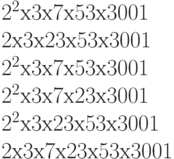
2 3 5 7 11 13	13360452 21949314 13360452 5797932 43898628 153645198	$2^2 х 3 х 7 х 53 х 3001\\ 2х3х23х53х3001\\2^2 х 3 х 7 х 53 х 3001\\ 2^2 х 3 х 7 х 23 х 3001\\2^2 х 3 х 23 х 53 х 3001\\ 2х3х7х23х53х3001$

g

order of g

factorization оГ the order

2

3

5

7

11

13

13360452

21949314

13360452

5797932

43898628

153645198

$2^2 х 3 х 7 х 53 х 3001\\ 2х3х23х53х3001\\2^2 х 3 х 7 х 53 х 3001\\ 2^2 х 3 х 7 х 23 х 3001\\2^2 х 3 х 23 х 53 х 3001\\ 2х3х7х23х53х3001$

Мы не приводим здесь порядок g = 4, так как, будучи квадратом числа 2, его порядок вдвое меньше порядка числа 2. В абелевой группе порядок произведения является делителем наименьшего общего кратного порядков множителей. По этой причине мы перечисляем только порядки простых элементов g.

Опять-таки, в реальной ситуации факторизация порядков недоступна, но крайне полезно при обучении взглянуть на них. Даже если факторизация порядков недоступна, все же возможно эффективно вычислить наименьшее общее кратное порядков, так как:

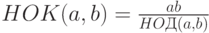
$HOK(a,b)=\frac{ab}{HOД(a,b)}$

а наибольший общий делитель - НОД(а, b) - эффективно вычисляется алгоритмом Эвклида.

Из теоремы Лагранжа следует, что М делится на наименьшее общее кратное порядков элементов. Для элементов, перечисленных выше, НОК равно:

R = 307290396 = 2^2 х 3 х 7 х 23 х 53 х 3001 = НОК(р - 1, q - 1).

В применениях к криптографии числа (р - 1) и (q - 1) имеют большие простые множители, в противном случае известны обычные, не квантовые методы взлома RSА. Из этого следует, что НОК(р -1, q -1) отличается от М только небольшим множителем. Так как 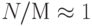$N/М \approx 1$ , то можно определить этот множитель из $N/ R = \frac{1843829587}{307290396}\approx 6.00028$ , следовательно, М = 6R

Так что, если нам удастся определить порядки элементов группы Z_N^* , то мы сможем факторизовать N. В оставшейся части этой главы мы сосредоточимся на проблеме нахождения порядка m заданного элемента g в Z_N^* ~.

Начнем с установки числа кубитов, которые требуются для квантового алгоритма. Выберем n такое, что $2^{n-1} < N < 2$ . Квантовый алгоритм, который мы собираемся описать, будет оперировать с 3n-кубитами.

Вначале инициализируем 3n-кубиты нулевыми значениями 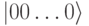$|00\dots 0\rangle$ .

Шаг 1. Применим трансформацию Адамара Н к каждому из первых 2п-кубитов:

$H|0\rangle \dots H|0\rangle|0\dots0\rangle=\frac{1}{\sqrt2}(|0\rangle+|1\rangle)\dots\frac{1}{\sqrt2}(|0\rangle+|1\rangle)|0\dots 0\rangle=\frac{2}{2^n}\sum_{k=0}^{2^{2n}-1}|k\rangle|0\dots0\rangle$

Шаг 2. Для заданного остатка g в Z_N^* рассмотрим функцию:

$f:B_{2n}\to B_n,\\ F(k)=g^k\; mod\; N,\;\;0\le k <2^{2n}$

Давайте покажем, что функция f - периодическая с периодом равным порядку элемента g. Так как этот порядок (который мы хотим определить) не превышает N, вычислим эту функцию на большом числе ее периодов. Классически это было бы недоступно, но на квантовом компьютере такое становится возможным благодаря массивному параллелизму квантовых вычислений.

Классическое вычисление f имеет квантовую реализацию 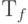Т_f , представляющую линейную трансформацию пространства 3n-кубита, где первые 2n битов являются входными битами, а последние n битов задают выход. Так как N < 2^n , то у нас достаточно числа бит, чтобы записать любой остаток по модулю N.

Применим 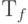Т_f к кубитам, сконструированным на Шаге 1:

$T_f\left(\frac{1}{2^n}\sum_{k=0}^{2^{2n}-1}|k\rangle|0\dots0\rangle\right)= \frac{1}{2^n}\sum_{k=0}^{2^{2n}-1}|k\rangle }g^k\; mod\; N\rangle$

Шаг З. Выполним измерения последних n битов. Результат этих измерений - вероятностный. Мы будем наблюдать одно из значений h, которое является степенью g по модулю N. Наш 3n-кубит сожмется в состояние, где последние n битов будут принимать значение h mod N. Что случится с первыми 2n битами? Все значения k такие, что 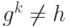$g^k \ne h$ , исчезнут. Все же, результирующее состояние будет включать сумму, так как есть больше чем одно значение k, для которого 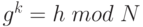$g^k = h\; mod\; N$ . Обозначим через s минимальное значение k.

Поскольку m - порядок у, то имеем:

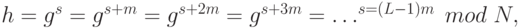
$h=g^s=g^{s+m}=g^{s+2m}=g^{s+3m}=\dots\g^{s=(L-1)m}\; mod\; N,$

где L - минимальное целое большее или равное 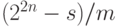$(2^{2n} - s)/m$ . Тогда квантовое состояние, полученное в результате этого измерения, может быть записано как:

$\frac{1}{\sqrtL}\sum_{j=0}^{L-1}|s+jm\rangle |h\rangle$

Мы видим, что коэффициенты в этом состоянии формируют последовательность, которая является периодической с периодом m (который и должен быть определен):

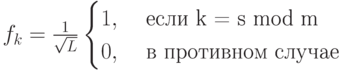
$f_k=\frac{1}{\sqrt{L}} \begin{cases} 1,&\text{ если k = s mod m}\\ 0,&\text{ в противном случае } \end{cases}$

Шаг 4. Применим квантовое преобразование Фурье к первым 2n битам. В результате получим состояние:

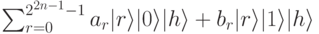
$\sum_{r=0}^{2^{2n-1}-1}a_r|r \rangle|0 \rangle|h \rangle+b_r|r \rangle|1 \rangle|h \rangle$

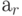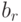где а_r и b_r . имеют пики в целых значениях, кратных частоте $\omega = 2^{2n}/m$ (смотри Упражнение в главе о дискретном преобразовании Фурье).

Шаг 5. Выполним измерения значений первых 2n - 1 битов. Результат измерений вероятностный с вероятностью наблюдения значения r, равной 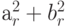а_r^2 + b_r^2 . С высокой вероятностью наблюдаемое значение r будет соответствовать пику и, следовательно, будет близко к целому числу, кратному $\omega = 2^{2n}/m$ .

Запишем наблюденное значение r и повторим Шаги 1-5 несколько раз, сохраняя наблюдения 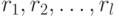$r_1,r_2,\dots,r_l$ , - здесь l - небольшое число. Это завершает квантовую часть алгоритма.

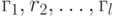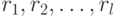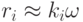Давайте опишем как можно определить значение m из наблюдаемых значений $г_1, r_2,\dots , г_l$ . Как мы отмечали, $r_1, r_2, \dots , r_l$ близки к целым кратным $\omega = 2^{2n}/m$ . Предположим, что $r_i\approx k_i\omega$ . Мы надеемся, что $НОД(k_1, \dots , k_l) = 1$ . Наши надежды вполне оправданы. В самом деле, вероятность того, что два больших случайных числа относительно просты, равна 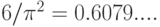$6/\pi^2 = 0.6079....$ Для l больших случайных чисел эта вероятность задается инверсией так называемой дзета-функции: 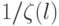$1/\zeta(l)$ . Например, для l= 6 вероятность того, что 6 случайных целых не имеют общего множителя равна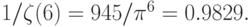 $1/\zeta(6) = 945/\pi^6 = 0.9829.$

Наша цель определить значение w, поскольку тогда просто определить m из соотношения 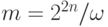$m = 2^{2n}/\omega$ . Хотя 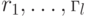$r_1, \dots , г_l$ - целые кратные $\omega$ , мы не можем использовать алгоритм Эвклида для поиска ы, хотя бы потому, что само значение $\omega$ не является целым числом. Поэтому давайте рассмотрим версию алгоритма Эвклида, которая находит приближенное значение НОД. Эта версия работает и для вещественных чисел.

Дальше >>

Авторизоваться

Квантовые вычисления

Алгоритм Шора

Вопросы и ответы