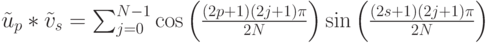Дискретное преобразование Фурье
Преобразование Фурье - это математический инструмент для изучения периодических или почти периодических функций. Хорошим примером почти периодических функций является звуковая волна, порождаемая звучанием музыкального инструмента. Давайте рассмотрим простейшее музыкальное устройство - вибрирующую струну Если "щипнуть" натянутую струну, то она начнет вибрировать и ее колебания порождают колебания воздуха вокруг струны.
В результате возникает звуковая волна, периодически распространяющаяся область высокого давления воздуха, сменяющаяся областью низкого давления. Эти волны распространяются в пространстве, удаляясь от источника звука. Для записи звука используется микрофон, имеющий внутри гибкую мембрану Сразу же как звуковая волна достигает микрофона, область высокого давления заставляет мембрану сжиматься, а низкого давления - тянет мембрану в обратном направлении. Микрофон преобразует колебания мембраны в электрический сигнал, который следует движениям мембраны. В аналоговой записи звука электрический сигнал может использоваться для намагничивания ленты, так что интенсивность магнитного поля ленты воспроизводит профиль звукового сигнала. В цифровой записи звука электрический сигнал, создаваемый микрофоном, измеряется. Измерения, проводимые с заданным временным интервалом, могут сохраняться в памяти компьютера. Например, для системы записи СD (компакт дисков) измерения проводятся с частотой 44100 Герц, что означает запись 44100 измерений в секунду Величина сигнала обычно масштабируется в интервале от-1 до 1.
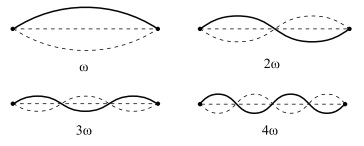
Давайте вернемся к обсуждению колеблющейся струны. Колеблющаяся струна издает звук с некоторой частотой, которая называется базовой частотой 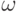 . Оказывается, что струна может колебаться более сложным способом. Она может иметь состояния высокой вибрации с частотой
. Оказывается, что струна может колебаться более сложным способом. Она может иметь состояния высокой вибрации с частотой 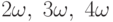 и так далее. На практике, колебание струны включает колебания высокой вибрации в дополнение к колебаниям с базовой частотой. В музыке,
и так далее. На практике, колебание струны включает колебания высокой вибрации в дополнение к колебаниям с базовой частотой. В музыке,
состояния высокой вибрации, производимые музыкальным инструментом, называются обертонами. Распределение интенсивности обертонов - это то, что отличает один инструмент от другого, играющего одну и ту же ноту.
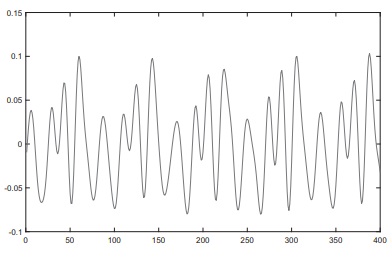
Ниже на рисунке представлена диаграмма звучания флейты, соответствующая примерно 0,01 секунды записи. Заметьте, что профиль почти периодический, - на диаграмме можно выделить 5 периодов.
Следующая диаграмма показывает спектр частот этой звуковой волны.
Поскольку это звук музыкального инструмента, играющего одну ноту, то диаграмма представляет пики, соответствующие базовой частоте (587 Нz; нота D второй октавы) и обертонам базовой частоты. Заметьте, для этого инструмента в частотном спектре отсутствует второй обертон.
Анализ частотного спектра сигнала, представленного выше, выполнен с использованием дискретного преобразования Фурье (ДПФ), которое мы намереваемся далее обсудить.
Давайте рассмотрим функцию  , определенную на интервале
, определенную на интервале 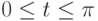 . Мы хотим измерить f(t) в N равноудаленных точках
. Мы хотим измерить f(t) в N равноудаленных точках 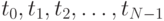 с расстоянием между точками равным
с расстоянием между точками равным  . Первую точку выберем не в 0, а в середине первого интервала - в точке
. Первую точку выберем не в 0, а в середине первого интервала - в точке 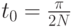 . Тогда
. Тогда 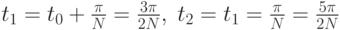 , и так далее с общей формулой:
, и так далее с общей формулой:
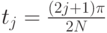
Последняя точка будет закрывать правый конец интервала:
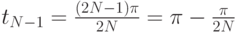
Измеряя f(t) в этих точках получим N-компонентный вектор
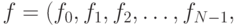
где 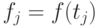 .
.
Далее будем полагать, что N четно, N = 2М.
Волны будем моделировать периодическими функциями cos(t) и sin(t). С этого момента будем полагать, что аргументы тригонометрических функций измеряются в радианах. Давайте рассмотрим семейство функций:
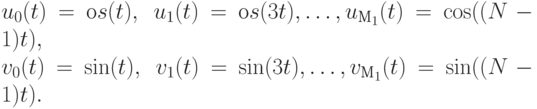
Мы можем записать их в более общей форме:
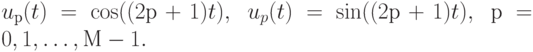
Используя измерения в ряде точек, можно перейти от непрерывных функций к их дискретным аналогам, создавая для каждой функции N-компонентный вектор:

Аналогично, выполним эти действия и для функции  .
.
Подставляя значения для точек 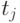 , получим:
, получим:
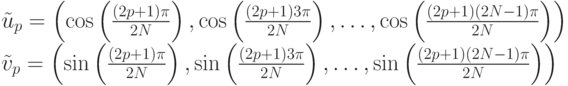
Здесь р принимает значения р = 0,1,..., М - 1.
В результате мы получили семейство из N векторов в 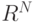 . Давайте изучим их свойства.
. Давайте изучим их свойства.
Теорема. Вектора 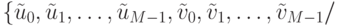 ортогональны друг другу и формируют базис в
ортогональны друг другу и формируют базис в 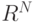
Прежде чем доказывать теорему, вспомним некоторые тригонометрические тождества.
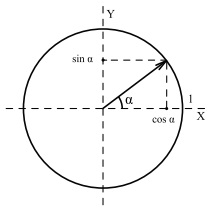
При рассмотрении свойств тригонометрических функций важно все время помнить, что 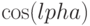 - это Х-координата точки единичного круга, соответствующая углу
- это Х-координата точки единичного круга, соответствующая углу  , в то время как
, в то время как 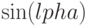 - это Y-координата той же точки. Из этого определения непосредственно следуют следующие свойства:
- это Y-координата той же точки. Из этого определения непосредственно следуют следующие свойства:
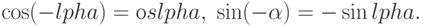
Только две тригонометрические формулы следует непосредственно держать в памяти:
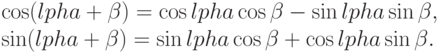
Все остальные тождества непосредственно выводимы. Изменяя знак  в предыдущих формулах, получим:
в предыдущих формулах, получим:
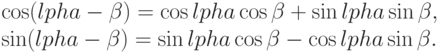
Комбинируя формулы, мы получим:

Нам понадобится следующее
Утверждение. Предположим 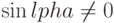 . Тогда
. Тогда

Для доказательства первого тождества нашего утверждения умножим его слева на 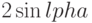 и применим формулу для
и применим формулу для 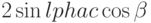
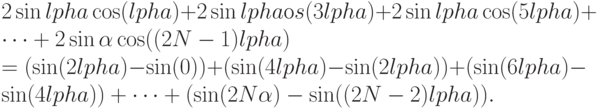
Большинство слагаемых в формуле будут взаимно уничтожаться, останется только 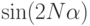 . Разделив обе стороны на
. Разделив обе стороны на 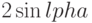 , получим первое тождество.
, получим первое тождество.
Доказательство второго тождества остается в качестве упражнения.
Доказательство теоремы. Для доказательства нам нужно вычислить скалярное произведение векторов нашего семейства:
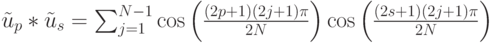
Применяя формулу для произведения косинусов, получим:

Далее, используя предыдущее утверждение вычислим сумму:
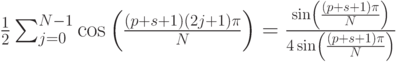
Эти вычисления справедливы при условии, что синус в знаменателе не равен нулю. Это так, поскольку  , откуда следует, что
, откуда следует, что 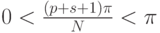 , следовательно, sin в знаменателе не равен нулю.
, следовательно, sin в знаменателе не равен нулю.
Вычисляя вторую сумму, получим:
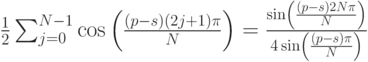
Эти вычисления также справедливы при условии, что синус в знаменателе не равен нулю. Здесь знаменатель превращается в ноль только тогда, когда р = s. Заметьте, что оба числителя в этом случае также равны нулю. Следовательно, когда 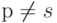 скалярное произведение
скалярное произведение  равно нулю. Если р = s, то первая сумма по-прежнему равна нулю, а во второй все косинусы равны 1, так что скалярное произведение векторов равно N/2. Давайте теперь вычислим скалярное произведение
равно нулю. Если р = s, то первая сумма по-прежнему равна нулю, а во второй все косинусы равны 1, так что скалярное произведение векторов равно N/2. Давайте теперь вычислим скалярное произведение