Блеск и нищета квантовых компьютеров
Закон Мура, сформулированный одним из основателей фирмы Intel Гордоном Муром, гласил, что число транзисторов интегральной схемы удваивается каждые два года. Это возможно при условии уменьшения размеров транзисторов. В 2017 году этот размер имел порядок 10 нанометров, что соответствует слою толщиной не более 50 атомов. Уже при этих масштабах становятся существенными квантовые эффекты, такие как квантовые туннельные эффекты, когда частица преодолевает барьер, который, согласно законам классической механики, она преодолеть не может из-за нехватки энергии.
Очевидно, что, следуя траектории закона Мура, принятая парадигма построения архитектуры компьютера должна натолкнуться на непроходимую стену, поскольку размер транзистора не может быть меньше межатомного расстояния в кристалле. Более того при приближении к барьеру, квантовые эффекты становятся определяющими.
В нашей повседневной жизни мы имеем дело с объектами, состоящими из многих атомов (число атомов в одной песчинке составляет примерно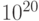 
. В больших коллекциях атомов квантовые эффекты взаимно поглощаются и в результате для макроскопических объектов нет необходимости в учете законов квантовой механики. И все же в современных технологиях растет интерес к использованию квантовых эффектов, например, светодиодные фонарики работают на основе квантовых принципов.
Идея квантовых вычислений основана на том, что не следует сражаться с влиянием квантовых эффектов, - необходимо научиться использовать возможности квантового мира. Это не просто, но дает большие преимущества. Квантовые компьютеры - это устройства, которые используют квантовые системы в качестве процессоров.
Какие же возможности открываются при использования квантовых компьютеров? В сравнении с обычными компьютерами мы получаем:
- память экспоненциально большого размера,
- возможность параллельно выполнять массивные вычисления. И снова скорость вычислений растет экспоненциально в сравнении с тем, что можно добиться для обычных классических компьютеров.
А что же мы теряем при этом?
- Исчезает прямой доступ к памяти. Акт чтения из квантовой памяти дает результат лишь с некоторой вероятностью, неизбежно разрушая при этом прочитанную запись.
- Квантовые процессоры должны быть полностью изолированы от окружающей среды при условии сохранении контроля и управления вычислениями.
- Отсутствует понимание и навыки создания эффективных квантовых алгоритмов, использующих всю мощь квантовых компьютеров.
Квантовые компьютеры имеют серьезную теоретическую базу как в физике, так и в математике. Однако проблемы их создания остаются весьма сложными и здесь для достижения успеха требуется существенный технологический прорыв.
Необходим существенный прогресс и в разработке квантовых алгоритмов. К счастью, для выполнения этой работы нет необходимости иметь настоящий работающий квантовый компьютер. Здесь достаточно пера, бумаги и понимания теории квантовых вычислений.
Давайте же попытаемся понять разницу между классическими и квантовыми компьютерами. В классическом компьютере данные хранятся в памяти в виде последовательности 0 и 1. Минимальной единицей памяти является бит, и он может хранить либо ноль, либо единицу Для целей нашего обсуждения 0 и 1 следует рассматривать как символы.
Единица памяти квантового компьютера называется кубит, и он может хранить одновременно как 0, так и 1. Более точно, значение кубита можно рассматривать как вектор единичной длины на плоскости:
Для установления связи с классическим битом пометим горизонтальную ось символом 0, а вертикальную -1. Соответственно для единичных векторов, расположенных на наших координатных осях, будем использовать нотацию, традиционную для квантовой механики:
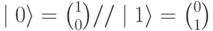
Тогда значение кубита может быть записано как:
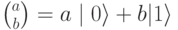
Значение кубита в этом случае можно интерпретировать как суперпозицию с весами а и b двух классических битов 0 и 1, где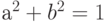 
. Заметьте, что мы рассматриваем здесь 
не как вектор длины 0, а как вектор единичной длины, расположенный на оси, помеченной символом "0".
Когда мы строим компьютер как физическую машину, нам необходимо использовать физические объекты, способные реализовать абстрактные конструкции бита и кубита. Конденсатор (электронное устройство, способное сохранять электрический заряд) может служить в качестве единицы памяти классического компьютера. Заряженное состояние конденсатора может рассматриваться как 1, а разряженное- 0.
Фотон может рассматриваться как физическая реализация кубита. Фотон - это квант электромагнитной волны. Представьте фотон, летящий в трехмерном пространстве вдоль оси Z. В процессе полета возникает колебание (осцилляция) электрического и магнитного полей во взаимно перпендикулярных направлениях в плоскости ХУ
Специфический способ проявления осцилляции называется поляризацией фотона. Существуют два возможных типа поляризация - круговая и линейная. При круговой поляризации при перемещении фотона направление электрического поля вращается в плоскости ХУ В этом курсе мы будем рассматривать только простейший случай линейной поляризации, когда электрическое поле осциллирует в фиксированном направлении перпендикулярно оси Z. Линейно поляризованные фотоны могут быть получены пропусканием светового потока через поляризационный фильтр.