Группы Ли
или
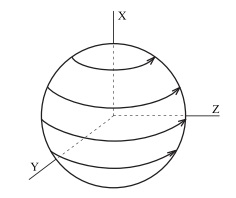
В случае (За) Т - отражение относительно плоскости, натянутой на вектора u, v. В случае (3b) Т - поворот вокруг v на угол 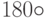 .
.
Обобщая эти результаты, формулируем:
Теорема. Ортогональная трансформация  - это либо пространственный поворот вокруг некоторой оси, либо композиция такого поворота с отражением в плоскости, ортогональной оси вращения.
- это либо пространственный поворот вокруг некоторой оси, либо композиция такого поворота с отражением в плоскости, ортогональной оси вращения.
Квантовый алгоритм представляет ортогональную трансформацию в 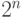 размерном пространстве n-кубитов. По этой причине мы заинтересованы в понимании структуры ортогональных трансформаций в пространствах произвольной размерности. Их описание дается следующей теоремой, которую мы представляем без доказательства. Доказательство не трудно, но требует привлечения более сложных средств линейной алгебры.
размерном пространстве n-кубитов. По этой причине мы заинтересованы в понимании структуры ортогональных трансформаций в пространствах произвольной размерности. Их описание дается следующей теоремой, которую мы представляем без доказательства. Доказательство не трудно, но требует привлечения более сложных средств линейной алгебры.
Прежде чем сформулировать теорему в качестве разминки попробуем ответить на следующий вопрос: возможно ли в 4-мерном пространстве иметь две 2-мерные плоскости, пересекающиеся в одной точке? Этот вопрос бросает вызов нашим представлениям о визуализации, так как наша интуиция основана на понимании 3-мерного мира, где плоскости пересекаются по прямой линии. И все же в 4-мерном пространстве плоскости могут пересекаться в одной точке. Для иллюстрации достаточно простого примера. Рассмотрим 4-мерное пространство с осями ХYZW. Тогда плоскость ХY содержит вектора, у которых две последние координаты равны 0, в то время как у векторов в плоскости ZW равны 0 первые две координаты. Очевидно, что пересечением этих двух 2-мерных плоскостей является единственная точка - начало координат.
Теорема. Для любой ортогональной трансформации Т в 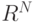 можно найти подпространства
можно найти подпространства 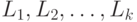 , такие что:
, такие что:
(1) Каждое подпространство 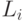 имеет размерность 1 или 2.
имеет размерность 1 или 2.
(2) Все подпространства 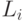 взаимно ортогональны и пересекаются только в начале координат.
взаимно ортогональны и пересекаются только в начале координат.
(3) Каждое подпространство 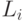 инвариантно относительно трансформации Т. Это значит, что Т преобразует вектора из
инвариантно относительно трансформации Т. Это значит, что Т преобразует вектора из 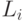 в вектора в том же подпространстве
в вектора в том же подпространстве 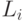 .
.
(4) Если 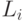 1-мерное подпространство, то Тv = v или Тv = -v для каждого вектора в
1-мерное подпространство, то Тv = v или Тv = -v для каждого вектора в 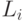 .
.
(5) Если 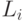 2-мерное подпространство, то Т действует как трансформация поворота плоскости
2-мерное подпространство, то Т действует как трансформация поворота плоскости 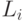 .
.
Давайте на примере 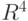 проиллюстрируем эту теорему Для данной ортогональной трансформации Т используем подпространства
проиллюстрируем эту теорему Для данной ортогональной трансформации Т используем подпространства 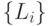 , чтобы сконструировать ортонормальный базис в
, чтобы сконструировать ортонормальный базис в 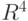 . В этом случае матрица Т должна быть одного из следующих типов:
. В этом случае матрица Т должна быть одного из следующих типов:
(а) Диагональная матрица с элементами  по диагонали. Это соответствует случаю, когда
по диагонали. Это соответствует случаю, когда 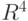 декомпозируется в четыре 1-мерные подпространства:
декомпозируется в четыре 1-мерные подпространства:
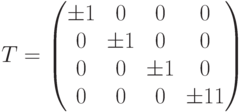
(b) Если  декомпозируется в 2-мерное инвариантное подпространство и два 1-мерных инвариантных подпространства, то матрица имеет вид:
декомпозируется в 2-мерное инвариантное подпространство и два 1-мерных инвариантных подпространства, то матрица имеет вид:
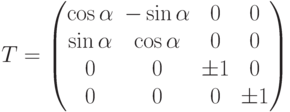
(с) Наконец,  может быть декомпозировано в два 2-мерных инвариантных подпространств. В этом случае Т представляет двойной поворот. (Попытайтесь визуализировать этот случай.)
может быть декомпозировано в два 2-мерных инвариантных подпространств. В этом случае Т представляет двойной поворот. (Попытайтесь визуализировать этот случай.)
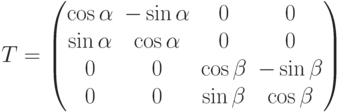
Как мы уже указывали, квантовый алгоритм задается ортогональной трансформацией в 2n-пространстве n-кубитов. При реализации алгоритма он рассматривается как последовательность элементарных трансформаций, каждая из которых затрагивает один или два кубита. Здесь есть полная аналогия с классическими алгоритмами, которые также представляют последовательность шагов, на каждом из которых выполняется элементарная операция. Алгебраически, декомпозиция квантового алгоритма представление большой ортогональной матрицы в виде произведения некоторых элементарных матриц.
Возможность подобной факторизации впервые была показана Эйлером в 1774 году, кто изучал факторизацию ортогональных матриц в 3-мерном пространстве. Эйлером доказана следующая
Теорема. Любой поворот в 3 мерном пространстве с координатными осями ХYZ может быть факторизован в виде композиции поворотов-поворота вокруг оси Х на угол  , поворота вокруг оси Y на угол
, поворота вокруг оси Y на угол  , еще одного поворота вокруг оси Х на угол
, еще одного поворота вокруг оси Х на угол  .
.
Параметры 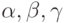 называются углами Эйлера для заданного поворота. Теорема Эйлера говорит, что достаточно иметь возможность осуществлять повороты вокруг осей Х и Y, чтобы генерировать любой поворот в пространстве
называются углами Эйлера для заданного поворота. Теорема Эйлера говорит, что достаточно иметь возможность осуществлять повороты вокруг осей Х и Y, чтобы генерировать любой поворот в пространстве
Алгебраически, эта теорема говорит, что матрица любого 3-мерного поворота может быть факторизована следующим образом:
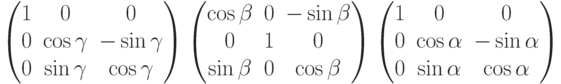
Для доказательства этой теоремы проще дать геометрическую интерпретацию, не прибегая к алгебраическим инструментам. Зафиксируем поворот Т. Предположим, что Т преобразует ортогональные оси  в координатные оси ХYZ. Заметим, что достаточно проследить за поведением двух осей. Если есть поворот, преобразующий
в координатные оси ХYZ. Заметим, что достаточно проследить за поведением двух осей. Если есть поворот, преобразующий  в Х, а
в Х, а 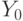 в Y, то автоматически
в Y, то автоматически 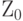 будет преобразовано в Z, так как повороты сохраняют углы между осями.
будет преобразовано в Z, так как повороты сохраняют углы между осями.
Цель первого шага-повернуть  вокруг оси Х, переходя к осям
вокруг оси Х, переходя к осям 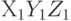 так, чтобы ось
так, чтобы ось 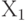 стала перпендикулярной оси Y. Это возможно, поскольку мы можем повернуть любой ненулевой вектор вокруг оси Х так, чтобы в результате вектор стал принадлежать плоскости ХZ.
стала перпендикулярной оси Y. Это возможно, поскольку мы можем повернуть любой ненулевой вектор вокруг оси Х так, чтобы в результате вектор стал принадлежать плоскости ХZ.
На втором шаге выполняем поворот вокруг оси Y, трансформируя 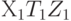 в
в 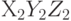 так, чтобы ось
так, чтобы ось 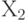 совпала с осью Х. Это возможно, поскольку ось
совпала с осью Х. Это возможно, поскольку ось 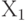 лежит в плоскости XZ после выполнения первого шага.
лежит в плоскости XZ после выполнения первого шага.
В завершение выполняем поворот вокруг оси Х так, чтобы новая ось 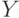 3 совпала с осью Y. Теперь
3 совпала с осью Y. Теперь 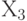 совпадает с Х,
совпадает с Х, 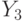 совпадает с Y, а, следовательно,
совпадает с Y, а, следовательно, 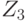 совпадает с Z.
совпадает с Z.