Лекция 12: Сходимость последовательностей случайных величин
Неравенства Чебышёва
Чтобы доказывать сходимость по вероятности, требуется
уметь вычислять 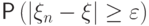 при больших
при больших  .
Но для этого нужно знать распределение
.
Но для этого нужно знать распределение 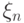 , что не всегда
возможно.
, что не всегда
возможно.
Полезно иметь неравенства, позволяющие оценивать
вероятность 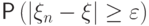 сверху. Тогда для доказательства сходимости по вероятности
было бы достаточно устремить к нулю эту оценку.
сверху. Тогда для доказательства сходимости по вероятности
было бы достаточно устремить к нулю эту оценку.
Все неравенства в этом параграфе принято относить к одному классу неравенств Чебышёва.
Теорема 35 (неравенство Маркова).
Если  , то для любого
, то для любого 

Доказательство. Нам потребуется следующее понятие.
Определение 44.
Назовем индикатором события  случайную
величину
случайную
величину  , равную единице, если событие
, равную единице, если событие  произошло, и
нулю,
если
произошло, и
нулю,
если  не произошло.
не произошло.
По определению, величина  имеет распределение Бернулли
с параметром
имеет распределение Бернулли
с параметром  и ее математическое ожидание равно вероятности успеха
и ее математическое ожидание равно вероятности успеха 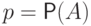 .
Индикаторы прямого и противоположного событий связаны равенством
.
Индикаторы прямого и противоположного событий связаны равенством 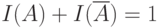 .
Поэтому
.
Поэтому

 .
Осталось разделить обе части этого неравенства на положительное число
.
Осталось разделить обе части этого неравенства на положительное число  .
.Следствие 16 (обобщенное неравенство
Чебышёва).
Пусть функция  не убывает и неотрицательна на
не убывает и неотрицательна на  .
Если
.
Если 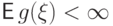 , то для любого
, то для любого 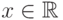

Доказательство.
Заметим, что  ,
поскольку функция
,
поскольку функция  не убывает. Оценим
последнюю вероятность по неравенству Маркова, которое можно применять
в силу неотрицательности
не убывает. Оценим
последнюю вероятность по неравенству Маркова, которое можно применять
в силу неотрицательности  :
:
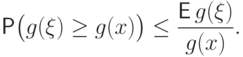
Упражнение.
Записать предыдущее неравенство для функции  и получить
экспоненциальное неравенство Чебышёва.
и получить
экспоненциальное неравенство Чебышёва.
Следствие 17 (неравенство Чебышёва).
Если  существует, то для любого
существует, то для любого 

Доказательство.
Для  неравенство
неравенство  равносильно неравенству
равносильно неравенству  , поэтому
, поэтому

Неравенство Чебышёва позволяет, помимо всего прочего, получать абсолютные
оценки для вероятности того, что стандартизованная случайная величина
превзойдет некоторое значение: для любого 
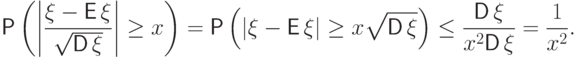
 эта вероятность не превышает
эта вероятность не превышает 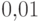 .
.