Классические и квантовые коды
Симплектические (стабилизирующие) коды [26]
Это аналог классических линейных кодов. Квантовые симплектические коды устроены так же, только вместо контрольных сумм будут использоваться 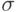 -операторы (
-операторы ( 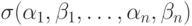 в предыдущих обозначениях).
в предыдущих обозначениях).
Зададим, например, таким способом код Шора. Для него  ,
, 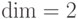 . Кодовое подпространство порождено двумя векторами, см. (14.11).
. Кодовое подпространство порождено двумя векторами, см. (14.11).
Каким условиям удовлетворяют базисные векторы  ?
?
- Для любых
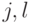
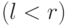 выполнено
выполнено 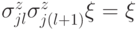 , т.е. каждая строка состоит из повторений одного бита.
, т.е. каждая строка состоит из повторений одного бита. - Для любого
 выполнено
выполнено 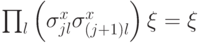 . Что означает это условие? Оператор
. Что означает это условие? Оператор 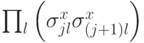 переводит(остальные строки не меняются). Эти два вектора должны входить в
переводит(остальные строки не меняются). Эти два вектора должны входить в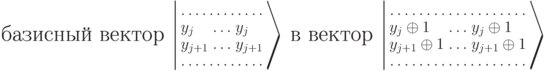
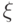 с одинаковыми коэффициентами.
с одинаковыми коэффициентами.
Утверждение 14.4. Если 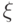 удовлетворяет условиям 1 и 2, то
удовлетворяет условиям 1 и 2, то 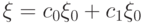 .
.
Прежде чем перейти к изучению более общих симплектических кодов, рассмотрим подробнее свойства 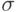 -операторов.
-операторов.
Как уже говорилось, 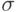 -операторы удобно индексировать элементами группы
-операторы удобно индексировать элементами группы 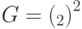 . Будем обозначать мультииндекс
. Будем обозначать мультииндекс 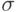 -оператора через
-оператора через 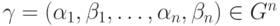 .
.
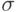 -операторы образуют базис в
-операторы образуют базис в 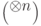 , более того, есть естественная
, более того, есть естественная 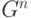 -градуировка:
-градуировка:

Для 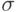 -операторов выполнены следующие соотношения
-операторов выполнены следующие соотношения
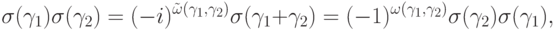
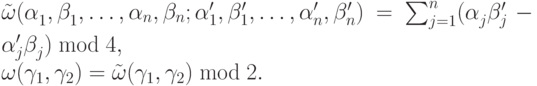
Рассмотрим унитарные преобразования — действия унитарных операторов  . Такое действие не меняется при домножении
. Такое действие не меняется при домножении  на число, равное по модулю единице, поэтому группа унитарных преобразований имеет вид
на число, равное по модулю единице, поэтому группа унитарных преобразований имеет вид 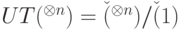 . Отметим, что унитарные преобразования — это в точности автоморфизмы
. Отметим, что унитарные преобразования — это в точности автоморфизмы  -алгебры
-алгебры 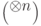 .
.
Нас интересуют такие преобразования, для которых  (
( 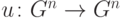 — некоторая функция). Оператор
— некоторая функция). Оператор 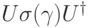 эрмитов, поэтому
эрмитов, поэтому  , то есть мы можем написать
, то есть мы можем написать
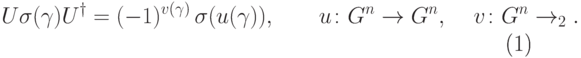 |
( 14.14) |
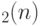 . Операторы из этой группы будем называть симплектическими. Приведем примеры.
. Операторы из этой группы будем называть симплектическими. Приведем примеры.-
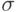 -операторы.
-операторы.  . В данном случае
. В данном случае 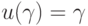 .
. - Оператор
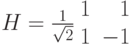 . Непосредственно проверяется, что
. Непосредственно проверяется, что 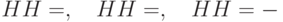 . Таким образом, преобразование
. Таким образом, преобразование  .
.
Можно показать, что  . Если учитывать фазовые множители, то получилась бы группа Клиффорда из
. Если учитывать фазовые множители, то получилась бы группа Клиффорда из 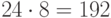 элементов.
элементов.
Основные свойства введенного отображения 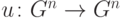 таковы:
таковы:
-
 линейно на
линейно на 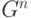 .
. -
 сохраняет форму
сохраняет форму 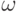 , т.е.
, т.е. 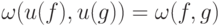 .
.
Отображения с такими свойствами, как известно, называются симплектическими; они образуют симплектическую группу 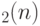 . Таким образом, определен гомоморфизм
. Таким образом, определен гомоморфизм 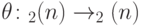 .
.
Теорема 14.3. 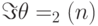 ,
, 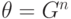 (ядро состоит из
(ядро состоит из 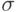 -операторов). Таким образом,
-операторов). Таким образом, 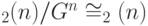 .
.
Для понимания доказательства желательно знать что-нибудь про расширения и когомологии групп [15]. Читателю, незнакомому с этими понятиями, будет предложен "обходной путь" (см. ниже).
Доказательство. Преобразование (14.14) должно быть автоморфизмом  -алгебры
-алгебры 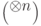 . Это имеет место тогда и только тогда, когда сохраняются правила умножения операторов
. Это имеет место тогда и только тогда, когда сохраняются правила умножения операторов  . Это означает, что функция
. Это означает, что функция  обладает указанными свойствами, а
обладает указанными свойствами, а 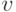 удовлетворяет уравнению
удовлетворяет уравнению
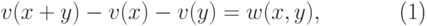 |
( 14.15) |
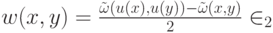 .
.В случае, когда  — тождественное отображение, правая часть уравнения (14.15) равна нулю. Решениями являются все линейные функции. Это доказывает, что
— тождественное отображение, правая часть уравнения (14.15) равна нулю. Решениями являются все линейные функции. Это доказывает, что 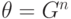 .
.
Утверждение 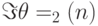 равносильно тому, что уравнение (14.15) имеет решение при любом
равносильно тому, что уравнение (14.15) имеет решение при любом  из
из 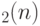 . Чтобы доказать это, заметим, что функция
. Чтобы доказать это, заметим, что функция  обладает следующими свойствами:
обладает следующими свойствами:
 |
( 14.16) |
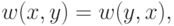 |
( 14.17) |
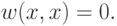 |
( 14.18) |
Формула (14.16) — это уравнение коцикла. Оно означает, что функция  задает структуру группы на декартовом произведении множеств
задает структуру группы на декартовом произведении множеств 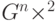 согласно правилу
согласно правилу 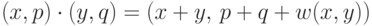 . Полученная группа (обозначим ее
. Полученная группа (обозначим ее 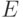 ) является расширением
) является расширением 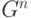 посредством
посредством 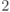 , т.е. определен гомоморфизм
, т.е. определен гомоморфизм 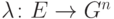 ,
, 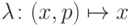 с ядром
с ядром 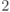 .
.
Уравнение (14.17) означает, что группа 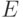 абелева. Наконец, уравнение (14.18) означает, что все элементы группы
абелева. Наконец, уравнение (14.18) означает, что все элементы группы 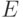 имеют порядок
имеют порядок 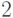 (или
(или  ). Следовательно,
). Следовательно, 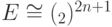 . Отсюда вытекает, что расширение
. Отсюда вытекает, что расширение  тривиально: существует гомоморфизм
тривиально: существует гомоморфизм 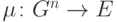 , такой что
, такой что 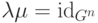 . Записывая этот гомоморфизм в виде
. Записывая этот гомоморфизм в виде 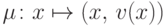 , получаем решение уравнения (14.15).
, получаем решение уравнения (14.15).
Существует другой, несколько кустарный способ доказать, что 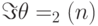 . Рассмотрим следующие симплектические преобразования:
. Рассмотрим следующие симплектические преобразования: ![(H\cdot H^\dagger)[j]](/sites/default/files/tex_cache/f4020e04e73d6eea376c6a2dd1f6fa6d.png) ,
, ![(K\cdot K^\dagger)[j]](/sites/default/files/tex_cache/d8c4ea2ecd91d4565435abf964e871c3.png) и
и ![\left(\Lambda(\sx)\cdot\Lambda^\dagger(\sx)\right)[j,k]](/sites/default/files/tex_cache/e5a863985a521fd4c84e10f865c25f8b.png) . (Напомним, что
. (Напомним, что 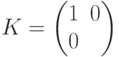 ). Их образы при гомоморфизме
). Их образы при гомоморфизме 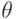 порождают всю группу
порождают всю группу 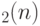 . (Намек на доказательство: любую пару векторов
. (Намек на доказательство: любую пару векторов 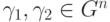 , такую что
, такую что 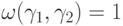 , можно перевести этими преобразованиями в
, можно перевести этими преобразованиями в 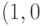 ,
, 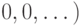 и
и 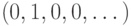 .) На самом деле, таким способом можно получить и другой интересный результат. Указанные элементы группы
.) На самом деле, таким способом можно получить и другой интересный результат. Указанные элементы группы 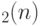 порождают все матрицы Паули, т.е. ядро гомоморфизма
порождают все матрицы Паули, т.е. ядро гомоморфизма 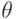 . Следовательно, верно такое утверждение.
. Следовательно, верно такое утверждение.
Утверждение 14.5. Группа 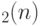 порождается элементами
порождается элементами
![(H\cdot H^\dagger)[j],\ (K\cdot K^\dagger)[j],\ \left(\Lambda(\sx)\cdot\Lambda^\dagger(\sx)\right)[j,k].](/sites/default/files/tex_cache/b683c4a25cda50c3633aa07872e2b116.png)
Для примера посмотрим на действие оператора ![U= \Lambda(\sx)[1,2]](/sites/default/files/tex_cache/16e17dd02c0104752ee61ebfed06561f.png) . По определению имеем
. По определению имеем  . Действие
. Действие 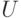 на образующие алгебры
на образующие алгебры  :
:
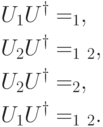
 можно понимать как измерение значения соответствующего q-бита. Первые два равенства просто показывают, как меняются эти значения при замене базиса, задаваемой
можно понимать как измерение значения соответствующего q-бита. Первые два равенства просто показывают, как меняются эти значения при замене базиса, задаваемой 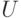 . Третье равенство показывает, что изменение значения второго q-бита коммутирует с заменой базиса
. Третье равенство показывает, что изменение значения второго q-бита коммутирует с заменой базиса 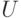 . Четвертое — что изменение значения первого q-бита при неизменном втором бите в повернутом базисе означает одновременное изменение значений обоих q-битов в исходном базисе.
. Четвертое — что изменение значения первого q-бита при неизменном втором бите в повернутом базисе означает одновременное изменение значений обоих q-битов в исходном базисе.Дадим теперь определение симплектического кода. В пространстве  мы выделим подпространство
мы выделим подпространство  условиями
условиями 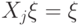 (
( 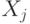 будем называть проверочными операторами ). Проверочные операторы будут иметь вид
будем называть проверочными операторами ). Проверочные операторы будут иметь вид
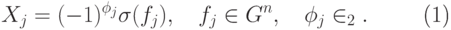 |
( 14.19) |
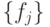 линейно независимы. Потребуем еще, чтобы все операторы
линейно независимы. Потребуем еще, чтобы все операторы 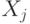 коммутировали. Поскольку
коммутировали. Поскольку 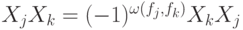 , условие коммутирования означает, что
, условие коммутирования означает, что 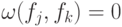 .
.Определение 14.9. Симплектический квантовый код задается условиями (14.19), где все 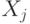 коммутируют.
коммутируют.
Итак, симплектическому квантовому коду соответствует изотропное подпространство 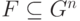 ; изотропность означает, что для любых
; изотропность означает, что для любых 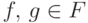 выполнено
выполнено 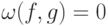 . Поэтому размерность симплектического кода легко вычисляется.
. Поэтому размерность симплектического кода легко вычисляется.
Теорема 14.4. 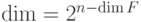 .
.
Лемма 14.6. Любой симплектический код приводится преобразованиями из 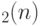 к стандартному виду, когда проверочными операторами являются
к стандартному виду, когда проверочными операторами являются ![\sigma^z[1],\dots,\sigma^z[s]](/sites/default/files/tex_cache/9cad7be5797f34f42701becb94c17c65.png) , где
, где 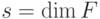 .
.
Доказательство. Подпространство 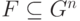 можно перевести отображением из
можно перевести отображением из 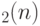 в подпространство
в подпространство 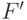 , состоящее из векторов вида
, состоящее из векторов вида 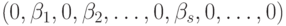 , где
, где 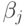 — произвольные. Согласно теореме 14.3, этому отображению соответствует некоторое унитарное преобразование
— произвольные. Согласно теореме 14.3, этому отображению соответствует некоторое унитарное преобразование 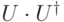 . Оно переводит кодовое подпространство в подпространство, заданное проверочными операторами
. Оно переводит кодовое подпространство в подпространство, заданное проверочными операторами ![\pm\sigma^z[j]](/sites/default/files/tex_cache/ccd061e86e0855c43cac8c9532163bfd.png) (
( 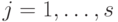 ). Применяя дополнительное преобразование вида
). Применяя дополнительное преобразование вида 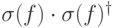 , все знаки можно сделать плюсами.
, все знаки можно сделать плюсами.
Теперь посмотрим, какие ошибки способен обнаруживать симплектический код. Напомним, что код обнаруживает ошибки из 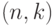 , если
, если
 |
( 14.20) |
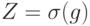 ,
,  .
.Пусть 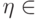 , т.е.
, т.е. 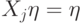 для всех
для всех 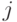 , где
, где 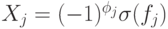 . Обозначим
. Обозначим 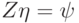 , где
, где 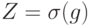 . Как мы сейчас увидим, вектор
. Как мы сейчас увидим, вектор 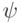 является собственным для всех проверочных операторов
является собственным для всех проверочных операторов 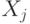 , поэтому он либо принадлежит кодовому подпространству
, поэтому он либо принадлежит кодовому подпространству  , либо ему
ортогонален. Подействуем проверочным оператором на
, либо ему
ортогонален. Подействуем проверочным оператором на 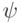 :
:
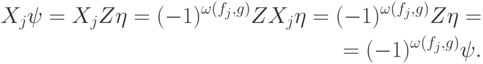
Условие 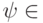 равносильно условию
равносильно условию 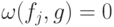 для всех
для всех 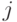 . Такие
. Такие 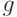 образуют линейное подпространство, которое мы обозначим
образуют линейное подпространство, которое мы обозначим 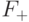 ,
т.е.
,
т.е. 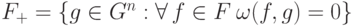 .
.
Возможны следующие три случая:
-
 . При этом
. При этом 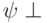 , поэтому
, поэтому 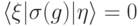 . Такую ошибку код обнаружит.
. Такую ошибку код обнаружит. -
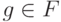 . Такая ошибка фактически неотличима от тождественного оператора, так как она не меняет кодового вектора
. Такая ошибка фактически неотличима от тождественного оператора, так как она не меняет кодового вектора 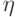 (с точностью до фазового множителя). Пусть
(с точностью до фазового множителя). Пусть  , тогда
, тогда 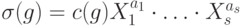 , где
, где 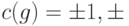 . В этом случае
. В этом случае 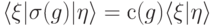 — условие (14.20) выполнено.
— условие (14.20) выполнено. -
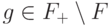 . В этом случае (проверьте!)
. В этом случае (проверьте!) 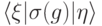 не имеет вида
не имеет вида  . Такую ошибку код не обнаруживает.
. Такую ошибку код не обнаруживает.
Этими рассуждениями доказана следующая теорема.
Теорема 14.5. Кодовое расстояние для симплектического кода 

Заметим отличие от классических линейных кодов. Там кодовое расстояние определяется как наименьшая норма вектора из подпространства с выкинутым нулем. А у симплектических кодов нуль раздувается до подпространства.
Задача 14.4. Постройте симплектический квантовый код типа 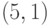 , исправляющий одну ошибку.
, исправляющий одну ошибку.
Задача 14.5. Докажите, что не существует квантового кода типа 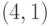 , исправляющего одну ошибку.
, исправляющего одну ошибку.
