Что такое алгоритм?
Неформально алгоритм — это однозначно определенная совокупность инструкций по преобразованию исходных данных в результат, причем все инструкции элементарны, т.е. при их выполнении "нам придется только механически следовать предписаниям, как если бы мы были роботами: от нас не потребуется ни понимания, ни искусства, ни изобретательности" [5, с. 270]. Формализовать это понятие можно различными способами.
Обычно подразумевается, что каждый алгоритм решает какую-то вычислительную задачу. С формальной точки зрения, вычислительная задача - это функция
F: входные данные -> результат,
Что такое "входные данные" и "результат"? Рассмотрим, например, задачу об умножении двух многочленов с целыми коэффициентами. Тогда входные данные - это пара многочленов. Проблема в том, как записать эти многочлены, чтобы их можно было ввести в компьютер. Машины Тьюринга, которые мы рассматриваем ниже, понимают лишь конечные последовательности символов (слова) из некоторого конечного множества A, называемого внешним алфавитом. Поэтому строгая формулировка вычислительной задачи должна включать в себя алфавит и способ кодировки входных данных. Например, можно записать пару многочленов с использованием 10 цифр, символа переменной x, знаков +, -, * и скобок: (x**2-5)(-4*x+1). В другой кодировке коэффициенты записываются в двоичной системе счисления и перечисляются через запятую; два многочлена разделяются звездочкой: 1, 0, -101* -100, 1. Таким образом, мы имеем две различные вычислительные задачи. С практической точки зрения, обе задачи эквивалентны, поскольку перевод из одной кодировки в другую осуществляется с помощью полиномиального алгоритма. Пока определения полиномального алгоритма у нас нет, давайте будем формалистами: вычислительная задача - это частичная1Под частичной функцией на множестве X здесь и далее понимается функция, область определения которой содержится в X. функция F: A* -> A* (где A* обозначает множество конечных слов в алфавите  ). Потом мы позволим себе некоторую вольность и будем говорить о задаче умножения многочленов или разложения целого числа на множители, имея ввиду, что все разумные кодировки эквивалентны (т.е. переводятся друг в друга при помощи полиномиальных алгоритмов). Однако нужно помнить, что не всякая кодировка является "разумной". Нехорошо, например, представлять натуральное число n набором из n звездочек, потому что длина такой записи экспоненциально велика по сравнению с двоичной или десятичной записью. Заметим также, что в некоторых задачах нет хорошего выбора "разумной" кодировки, в таких случаях (они нам не встретятся) необходимо указывать кодировку всякий раз, когда формулируется задача.
). Потом мы позволим себе некоторую вольность и будем говорить о задаче умножения многочленов или разложения целого числа на множители, имея ввиду, что все разумные кодировки эквивалентны (т.е. переводятся друг в друга при помощи полиномиальных алгоритмов). Однако нужно помнить, что не всякая кодировка является "разумной". Нехорошо, например, представлять натуральное число n набором из n звездочек, потому что длина такой записи экспоненциально велика по сравнению с двоичной или десятичной записью. Заметим также, что в некоторых задачах нет хорошего выбора "разумной" кодировки, в таких случаях (они нам не встретятся) необходимо указывать кодировку всякий раз, когда формулируется задача.
Теперь дадим формальное определение алгоритма.
Машины Тьюринга.
Машина Тьюринга (сокращенно МТ) однозначно задается указанием набора 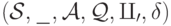 , где
, где 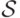 ,
, 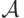 ,
,  — конечные множества, причем
— конечные множества, причем 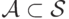 ;
;  — некоторый элемент
— некоторый элемент  ;
;  — некоторый элемент
— некоторый элемент  , а
, а  — некоторая (частичная, вообще говоря) функция из
— некоторая (частичная, вообще говоря) функция из  в
в 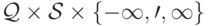 .
.
Составляющие части МТ называются так:
 — пустой символ (или пробел),
— пустой символ (или пробел),
 — множество состояний управляющего устройства,
— множество состояний управляющего устройства,
 — начальное состояние,
— начальное состояние,
Состояние МТ задается тройкой 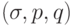 , где
, где  — бесконечное слово в алфавите
— бесконечное слово в алфавите 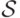 , т.е. произвольная последовательность
, т.е. произвольная последовательность 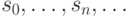 элементов
элементов 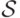 ;
;  — неотрицательное целое число;
— неотрицательное целое число; 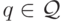 . Символы слова
. Символы слова  будем, как это принято, представлять записанными на ленте, разбитой на ячейки, по ячейке на символ. На ленте также имеется головка, которая расположена над ячейкой с номером
будем, как это принято, представлять записанными на ленте, разбитой на ячейки, по ячейке на символ. На ленте также имеется головка, которая расположена над ячейкой с номером  . Наглядно это изображается так:
. Наглядно это изображается так:
Помимо ленты машина Тьюринга имеет управляющее устройство, состояние которого задается элементом  множества
множества  .
.
Состояния МТ меняются дискретно. За один такт работы управляющее устройство выполняет следующие действия (полагаем, что МТ находится в состоянии 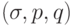 ):
):
-
читает символ, находящийся под головкой (т.е. определяет
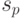 );
); -
вычисляет значение функции переходов:
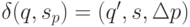 (если функция переходов на паре
(если функция переходов на паре 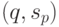 не определена, то останавливает машину Тьюринга);
не определена, то останавливает машину Тьюринга); -
записывает на ленту в ячейку
 символ
символ  , сдвигает головку на
, сдвигает головку на 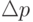 и переходит в состояние
и переходит в состояние 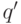 (другими словами, новое состояние машины задается тройкой
(другими словами, новое состояние машины задается тройкой  );
); -
если
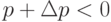 , то останавливает машину.
, то останавливает машину.
Пожалуй, всякий согласится, что эти действия не требуют ни понимания, ни искусства, ни изобретательности.
Работа машины Тьюринга будет всегда начинаться из состояния 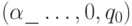 , где за конечным словом
, где за конечным словом  , состоящим из символов внешнего алфавита (множество таких слов обозначается
, состоящим из символов внешнего алфавита (множество таких слов обозначается 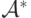 ), следует бесконечное слово, целиком состоящее из пустых символов. Слово
), следует бесконечное слово, целиком состоящее из пустых символов. Слово  будем называть входом МТ. В любой момент времени слово, записанное на ленте, однозначно записывается в виде
будем называть входом МТ. В любой момент времени слово, записанное на ленте, однозначно записывается в виде 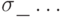 , где последний символ слова
, где последний символ слова  — не пустой, а за ним идут только пустые символы. Будем называть слово
— не пустой, а за ним идут только пустые символы. Будем называть слово  используемой частью ленты.
используемой частью ленты.
Выполняя один такт работы за другим, машина Тьюринга порождает последовательность состояний 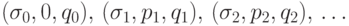
Если МТ останавливается, используемая часть ленты в достигнутом перед остановкой состоянии называется результатом работы МТ.

