Решения задач
Из раздела 1
1.1 Неформально описать такую машину легко. Она переносит символы по одному слева направо и справа налево, пока не обнаруживает, что достигнута середина слова, после чего останавливается.
Дадим теперь формальное описание этой машины.
Внешний алфавит: 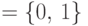 . Алфавит
. Алфавит 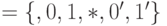 , помимо символов внешнего алфавита и пустого символа
, помимо символов внешнего алфавита и пустого символа  , включает три вспомогательных метки, указывающих на положение символов, которые переносятся.
, включает три вспомогательных метки, указывающих на положение символов, которые переносятся.
Множество состояний управляющего устройства
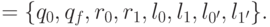
 и
и  указывают на направление переноса символа, индексы при этих буквах — на переносимый символ.
указывают на направление переноса символа, индексы при этих буквах — на переносимый символ.Теперь зададим функцию переходов. Для всех пар, на которых функция переходов не определена приводимыми ниже правилами, ее значения можно выбирать произвольно.
Начало работы:
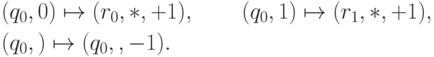
Перенос вправо:

Перемена направления движения справа налево состоит из двух действий: снять метку (если это не пустой символ)
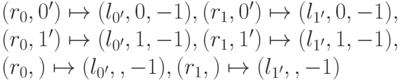
и поставить ее на левого соседа
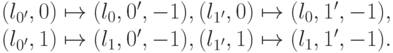
Перенос влево:

Перемена движения слева направо:

Завершение работы зависит от четности длины слова: при четной длине остановка происходит при начале движения вправо
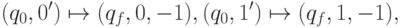
а при нечетной длине — при начале движения влево
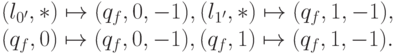
1.2 Неформально делается следующее: ко второму слагаемому поочередно добавляются разряды первого, добавленный разряд стирается. Добавление одного разряда происходит за время, не превышающее удвоенной длины второго слагаемого, так что общее время работы машины квадратично зависит от длины входа.
Дадим теперь формальное описание такой машины.
Внешний алфавит: 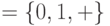 . Алфавит
. Алфавит 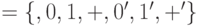 , помимо символов внешнего алфавита и пустого символа
, помимо символов внешнего алфавита и пустого символа  , включает три вспомогательных метки.
, включает три вспомогательных метки.
Множество состояний управляющего устройства
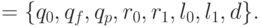
 и
и  указывают на направление переноса символа, индексы при этих буквах — на переносимый символ (влево машина носит бит переноса в следующий разряд, а вправо — добавляемый бит), в состоянии
указывают на направление переноса символа, индексы при этих буквах — на переносимый символ (влево машина носит бит переноса в следующий разряд, а вправо — добавляемый бит), в состоянии  машина осуществляет стирание обработанного разряда.
машина осуществляет стирание обработанного разряда.Теперь зададим функцию переходов. Как и в задаче 1.1, для не упомянутых ниже пар функция переходов определена произвольно.
Начало и конец работы:
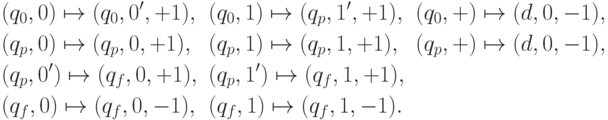
 . Если найден знак
. Если найден знак 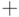 , то происходит переход к началу добавления очередного слагаемого. Если найдена метка, то она стирается, а машина останавливается. При этом на ленте остается результат сложения (считаем, что сумма может начинаться нулями).
, то происходит переход к началу добавления очередного слагаемого. Если найдена метка, то она стирается, а машина останавливается. При этом на ленте остается результат сложения (считаем, что сумма может начинаться нулями).Определение очередного бита, который нужно добавлять ко второму слагаемому, перенос его вправо и переход в режим сложения:
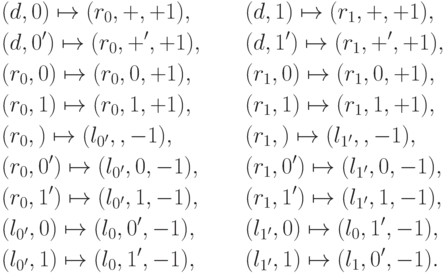
Сложение, пока не достигнут знак 
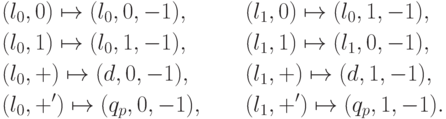
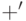 уже ничего нет. Поэтому машина начинает двигаться вправо, чтобы стереть оставшуюся метку.
уже ничего нет. Поэтому машина начинает двигаться вправо, чтобы стереть оставшуюся метку.1.3 Доказательство от противного. Предположим, что такой алгоритм есть, т.е. существует машина  , которая на входе
, которая на входе ![([М],x)](/sites/default/files/tex_cache/b9517a602e14479bad3f4fe56c899e07.png) дает ответ "да", если машина
дает ответ "да", если машина  останавливается на входе
останавливается на входе  , в противном случае дает ответ "нет" (через
, в противном случае дает ответ "нет" (через ![[М]](/sites/default/files/tex_cache/6203329e7453ebd52167d2dfc9426c5a.png) обозначено описание машины
обозначено описание машины  ). Тогда есть и такая машина
). Тогда есть и такая машина 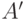 , которая на входе
, которая на входе  моделирует работу
моделирует работу  на входе
на входе  . Затем, если ответ машины
. Затем, если ответ машины  — "да", то
— "да", то 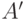 начинает двигать головку вправо и не останавливается, а если ответ
начинает двигать головку вправо и не останавливается, а если ответ  — "нет", то
— "нет", то 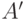 останавливается.
останавливается.
Остановится ли 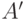 на входе
на входе ![[A']](/sites/default/files/tex_cache/381eedbc23a9a48b2ad5b9c93514a0a9.png) ? Если остановится, то
? Если остановится, то  дает ответ "да" на входе
дает ответ "да" на входе ![([A'],[A'])](/sites/default/files/tex_cache/b84517d11178749b0e9c6600633da900.png) . Тогда, по определению машины
. Тогда, по определению машины 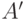 , на входе
, на входе ![[A']](/sites/default/files/tex_cache/381eedbc23a9a48b2ad5b9c93514a0a9.png) она не остановится. Итак,
она не остановится. Итак, 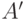 на входе
на входе ![[A']](/sites/default/files/tex_cache/381eedbc23a9a48b2ad5b9c93514a0a9.png) не останавливается. Но тогда
не останавливается. Но тогда  дает ответ "нет" на входе
дает ответ "нет" на входе ![([A'],[A'])](/sites/default/files/tex_cache/b84517d11178749b0e9c6600633da900.png) . Но это означает, что
. Но это означает, что 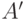 на входе
на входе ![[A']](/sites/default/files/tex_cache/381eedbc23a9a48b2ad5b9c93514a0a9.png) останавливается. Пришли к противоречию.
останавливается. Пришли к противоречию.
1.4 Во-первых, заметим, что есть алгоритм, который выписывает одну за другой те МТ, которые останавливаются, будучи запущенными на пустой ленте. Этот алгоритм перебирает все пары ![([M],n)](/sites/default/files/tex_cache/df01ea1a485fa4c71301858b2aae5e03.png) (
( ![[M]](/sites/default/files/tex_cache/73729d04b8e6f0a5d694ba46a855be7e.png) — описание машины
— описание машины  ,
,  — натуральное число) и для каждой пары моделирует работу
— натуральное число) и для каждой пары моделирует работу  на пустом входе в течение
на пустом входе в течение  тактов. Если за это время происходит остановка, то
тактов. Если за это время происходит остановка, то  включается в список, если не была включена в него ранее.
включается в список, если не была включена в него ранее.
Если бы существовал еще и такой алгоритм, который выписывает одну за другой машины, не останавливающиеся на пустом входе, то можно было бы построить и алгоритм, проверяющий, останавливается ли МТ  на пустом входе: запускаем оба алгоритма перечисления и ждем, когда описание
на пустом входе: запускаем оба алгоритма перечисления и ждем, когда описание  появится в одном или в другом списке.
появится в одном или в другом списке.
Но тогда существовал бы и алгоритм, решающий проблему остановки: по машине  и входу
и входу  легко строится машина, которая сначала записывает
легко строится машина, которая сначала записывает  на ленту, а затем моделирует работу
на ленту, а затем моделирует работу  . Так что из предыдущей задачи заключаем, что нет алгоритма, перечисляющего машины, не останавливающиеся на пустом слове.
. Так что из предыдущей задачи заключаем, что нет алгоритма, перечисляющего машины, не останавливающиеся на пустом слове.
1.5 Ограничимся указанием. Для любой вычислимой функции 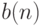 при достаточно больших
при достаточно больших  среди машин с
среди машин с  символами алфавита и
символами алфавита и  состояниями, останавливающихся на пустом входе, можно найти и такую, которая вычисляет
состояниями, останавливающихся на пустом входе, можно найти и такую, которая вычисляет 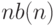 , а затем вычитает из этого числа по единице, пока не дойдет до нуля.
, а затем вычитает из этого числа по единице, пока не дойдет до нуля.
1.6 Пусть имеется двухленточная МТ  , работающая за время
, работающая за время 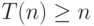 на входах длины
на входах длины  . Опишем неформально машину
. Опишем неформально машину 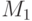 с единственной лентой, моделирующую работу
с единственной лентой, моделирующую работу  . Алфавит этой машины достаточно велик, чтобы кодировать в одной ячейке содержимое ячеек с тем же номером на лентах
. Алфавит этой машины достаточно велик, чтобы кодировать в одной ячейке содержимое ячеек с тем же номером на лентах  и информацию о положении головок (на каких лентах головки находятся над ячейкой с тем же номером). Управляющее устройство
и информацию о положении головок (на каких лентах головки находятся над ячейкой с тем же номером). Управляющее устройство 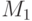 позволяет запоминать содержимое ячеек, над которыми находятся головки
позволяет запоминать содержимое ячеек, над которыми находятся головки  , и состояние управляющего устройства
, и состояние управляющего устройства  .
.
Машина 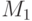 работает циклами, каждый из которых имитирует один такт работы
работает циклами, каждый из которых имитирует один такт работы  . В начале каждого цикла головка
. В начале каждого цикла головка 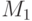 находится над самой левой ячейкой.
находится над самой левой ячейкой.
Цикл состоит из двух последовательных проходов по записанному слову. Вначале 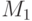 движется вправо и собирает информацию о состояниях в ячейках
движется вправо и собирает информацию о состояниях в ячейках  , над которыми находятся головки. При обратном проходе справа налево
, над которыми находятся головки. При обратном проходе справа налево 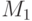 выполняет действия, имитирующие такт работы
выполняет действия, имитирующие такт работы  . На каждое такое действие требуется
. На каждое такое действие требуется 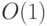 тактов.
тактов.
Цикл выполняется за  тактов работы
тактов работы 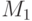 , где
, где  — длина используемой части ленты. Так как
— длина используемой части ленты. Так как 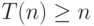 , то
, то 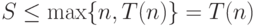 . Поэтому
. Поэтому 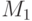 работает за время
работает за время 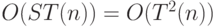 .
.
1.7 Приведем еще более неформальное, чем в предыдущей задаче, описание алгоритма. Алфавит моделирующей машины выберем достаточно большим, чтобы кодировать в одной ячейке содержимое ячеек на всех лентах, информацию о положении головок (на каких лентах головки находятся над данной ячейкой) и дополнительные метки, которые потребуются в процессе работы.
Опишем алгоритм  , который решает такую задачу: на одной из лент записано слово
, который решает такую задачу: на одной из лент записано слово 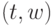 , на второй головка находится в конце используемой части ленты, нужно промоделировать работу трехленточной машины за период времени
, на второй головка находится в конце используемой части ленты, нужно промоделировать работу трехленточной машины за период времени  (записанный двоичным словом), если вначале состояние лент определено словом
(записанный двоичным словом), если вначале состояние лент определено словом  .
.
Запишем на свободное место на второй ленте число 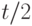 , после чего скопируем туда же
, после чего скопируем туда же  -окрестности каждой из головок на всех трех лентах исходной машины и переместим головку в конец слова
-окрестности каждой из головок на всех трех лентах исходной машины и переместим головку в конец слова  (в конец используемой части первой ленты). К полученному на второй ленте слову применим рекурсивно алгоритм
(в конец используемой части первой ленты). К полученному на второй ленте слову применим рекурсивно алгоритм  , по завершении его работы скопируем на первую ленту результат моделирования, скопируем на вторую ленту
, по завершении его работы скопируем на первую ленту результат моделирования, скопируем на вторую ленту  -окрестности головок во вновь полученном состоянии, отвечающем состоянию трехленточной машины после
-окрестности головок во вновь полученном состоянии, отвечающем состоянию трехленточной машины после 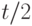 тактов работы, опять переместим головку в конец используемой части первой ленты. Еще раз рекурсивно применим
тактов работы, опять переместим головку в конец используемой части первой ленты. Еще раз рекурсивно применим  к слову на второй ленте, по завершении его работы скопируем результат моделирования на первую ленту.
к слову на второй ленте, по завершении его работы скопируем результат моделирования на первую ленту.
Для корректного описания алгоритма нужно еще задать его работу на слове 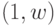 . В этом случае просто применяем алгоритм, аналогичный описанному в предыдущей задаче.
. В этом случае просто применяем алгоритм, аналогичный описанному в предыдущей задаче.
Операцию копирования с ленты на ленту можно осуществить за линейное от длины копируемого слова время. Поэтому для времени 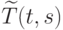 работы в наихудшем случае алгоритма
работы в наихудшем случае алгоритма  , моделирующего работу трехленточной машины за время
, моделирующего работу трехленточной машины за время  на словах длины
на словах длины  , получаем оценку:
, получаем оценку:
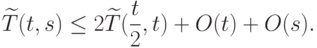 |
( *) |
 сразу следует, что при некоторой константе
сразу следует, что при некоторой константе 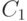 и
и 

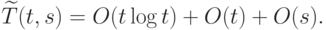
Заметим, что получить слово 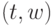 из слова
из слова  можно за время
можно за время 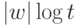 , если
, если  известно.
известно.
Алгоритм моделирования трехленточной машины на двухленточной использует алгоритм  следующим образом. Промоделируем работу машины из начального состояния за 1 такт, затем работу за 2 такта из достигнутого состояния и т.д. Оценим время работы этого алгоритма. Пусть исходная трехленточная машина работает на словах длины
следующим образом. Промоделируем работу машины из начального состояния за 1 такт, затем работу за 2 такта из достигнутого состояния и т.д. Оценим время работы этого алгоритма. Пусть исходная трехленточная машина работает на словах длины  за время
за время 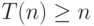 . Тогда время
. Тогда время 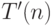 работы моделирующей машины будет оцениваться как
работы моделирующей машины будет оцениваться как
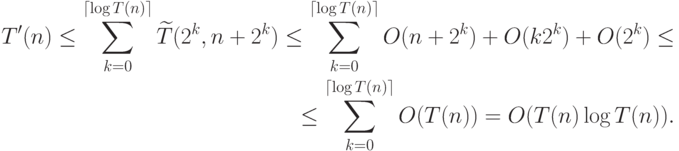
1.8 Информация в машине Тьюринга переносится головкой управляющего устройства. Более точно эта мысль формулируется так. Рассмотрим последовательность 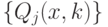 состояний управляющего устройства МТ в моменты переходов головки между
состояний управляющего устройства МТ в моменты переходов головки между  -й и
-й и 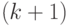 -й ячейками при работе МТ на входе
-й ячейками при работе МТ на входе  (рассматриваем переходы в обе стороны). Работа машины Тьюринга справа от
(рассматриваем переходы в обе стороны). Работа машины Тьюринга справа от  -й ячейки полностью определяется последовательностью
-й ячейки полностью определяется последовательностью 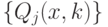 .
.
Теперь запишем нижнюю оценку на время работы МТ, копирующей входное слово. Она основана на том, что каждый переход головки требует отдельного такта работы МТ. Введем параметры 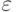 и
и 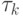 , значения которых определим позже. Для слова
, значения которых определим позже. Для слова  через
через 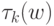 обозначим число переходов головки между
обозначим число переходов головки между  -й и
-й и 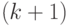 -й ячейками при работе МТ на входе
-й ячейками при работе МТ на входе  . Будем искать такое слово
. Будем искать такое слово  , что
, что 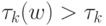 при
при 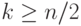 .
.
Поскольку МТ копирует начальный кусок длины  справа от
справа от  -й ячейки, последовательности
-й ячейки, последовательности 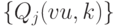 при фиксированном
при фиксированном  должны быть различны для различных
должны быть различны для различных  -буквенных слов
-буквенных слов  . Коротких (длины не больше
. Коротких (длины не больше  ) последовательностей состояний управляющего устройства не больше, чем
) последовательностей состояний управляющего устройства не больше, чем 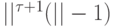 , где
, где  — множество состояний управляющего устройства. Для любого
— множество состояний управляющего устройства. Для любого 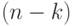 -буквенного слова
-буквенного слова  при
при
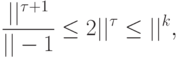 |
( *) |
 — внешний алфавит, неравенство
— внешний алфавит, неравенство 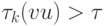 выполнено по крайней мере для доли
выполнено по крайней мере для доли 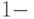 от всех
от всех  -буквенных слов
-буквенных слов  . Это означает, что для доли
. Это означает, что для доли 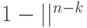 от всех
от всех  -буквенных слов
-буквенных слов  неравенство
неравенство 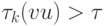 выполняется для всех
выполняется для всех  . Поэтому при
. Поэтому при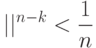 |
( **) |
 такое, что
такое, что 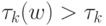 при
при 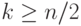 .
.Если 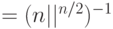 , то
, то  выполняется при
выполняется при 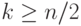 . Если при этом еще и
. Если при этом еще и  , то
, то  выполняется при
выполняется при 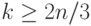 . При таком выборе параметров
. При таком выборе параметров  при
при 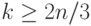 . Оценим время работы МТ на слове
. Оценим время работы МТ на слове  таком, что
таком, что 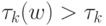 при
при 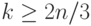 (мы уже доказали, что такое слово есть)
(мы уже доказали, что такое слово есть)
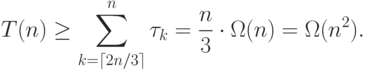
Для оценки минимального времени работы 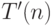 можно считать, что МТ вначале дописывает за
можно считать, что МТ вначале дописывает за 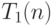 тактов последовательность из одних 0 длины
тактов последовательность из одних 0 длины  , затем за
, затем за  шагов проверяет, состоит ли исходное слово из одних 0, после чего прекращает работу, если это так, а в противном случае работает любым правильным способом. Ясно, что
шагов проверяет, состоит ли исходное слово из одних 0, после чего прекращает работу, если это так, а в противном случае работает любым правильным способом. Ясно, что 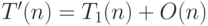 . В свою очередь,
. В свою очередь,  . Действительно, если бы машина во внутренней памяти могла хранить числа, то копирование слова из нулей не создало бы проблемы (надо было бы подсчитать длину слова и потом написать столько же нулей). Но этого сделать нельзя. Зато машина Тьюринга может хранить число в двоичной записи в окрестности своей головки (мы можем расширить алфавит и считать, что на ленте есть место для дополнительных пометок рядом с буквами слова из нулей и единиц). При этом прибавление единицы к такому счетчику, вычитание единицы и сдвиг счетчика по ленте (его ведь надо возить с собой) требуют времени порядка длины счетчика, т.е.
. Действительно, если бы машина во внутренней памяти могла хранить числа, то копирование слова из нулей не создало бы проблемы (надо было бы подсчитать длину слова и потом написать столько же нулей). Но этого сделать нельзя. Зато машина Тьюринга может хранить число в двоичной записи в окрестности своей головки (мы можем расширить алфавит и считать, что на ленте есть место для дополнительных пометок рядом с буквами слова из нулей и единиц). При этом прибавление единицы к такому счетчику, вычитание единицы и сдвиг счетчика по ленте (его ведь надо возить с собой) требуют времени порядка длины счетчика, т.е.  , так что всего мы укладываемся в
, так что всего мы укладываемся в  тактов.
тактов.
Замечание. Можно показать, что 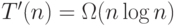 . Читателю предлагается самостоятельно понять, как нужно модифицировать изложенную выше нижнюю оценку времени работы в худшем случае.
. Читателю предлагается самостоятельно понять, как нужно модифицировать изложенную выше нижнюю оценку времени работы в худшем случае.
