Решения задач
2.6 б). Заметим, что число раскрасок в 3 цвета по очевидным причинам кратно 6: перестановка цветов сохраняет правильную раскраску.
Пусть есть 3-КНФ из  дизъюнкций, в которые входят
дизъюнкций, в которые входят  переменных. Граф, который сопоставляется этой КНФ, имеет
переменных. Граф, который сопоставляется этой КНФ, имеет 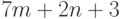 вершин. Для описания структуры графа удобно пометить часть вершин. Во-первых, пометим три вершины числами 0, 1, 2. Во-вторых, пометим каждым литералом (переменной или ее отрицанием) по одной вершине. Остальные
вершин. Для описания структуры графа удобно пометить часть вершин. Во-первых, пометим три вершины числами 0, 1, 2. Во-вторых, пометим каждым литералом (переменной или ее отрицанием) по одной вершине. Остальные 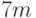 вершин разобьем на группы по 7, каждая группа соответствует одной из дизъюнкций.
вершин разобьем на группы по 7, каждая группа соответствует одной из дизъюнкций.
Теперь опишем ребра этого графа. Как показано на рис. 15.4а), вершины 0, 1 и 2 соединены между собой ребрами. На рис. 15.4б) показаны еще  треугольников в этом графе. И, наконец, рис. 15.4в) показывает, как соединены ребрами вершины, соответствующие каждой дизъюнкции. На этом рисунке
треугольников в этом графе. И, наконец, рис. 15.4в) показывает, как соединены ребрами вершины, соответствующие каждой дизъюнкции. На этом рисунке 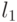 ,
, 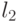 ,
, 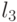 обозначают литералы, входящие в дизъюнкцию. Заметим, что некоторые ребра мы перечислили по нескольку раз.
обозначают литералы, входящие в дизъюнкцию. Заметим, что некоторые ребра мы перечислили по нескольку раз.
Очевидно, что описанное выше построение можно выполнить за полиномиальное от  и
и  время. Докажем его корректность.
время. Докажем его корректность.
Рассмотрим, какие правильные раскраски в 3 цвета возможны для такого графа. Без ограничения общности можно считать, что вершины 0, 1 и 2 покрашены в цвета 0, 1 и 2 (из шести раскрасок, различающихся перестановками цветов мы выбрали одну). Тогда вершины, помеченные  и
и  , покрашены в цвета 0 и 1, причем их цвета должны быть противоположны (см. рис. 15.4б).
, покрашены в цвета 0 и 1, причем их цвета должны быть противоположны (см. рис. 15.4б).
Прямым перебором вариантов можно проверить, что граф, изображенный на рис. 15.4в) удовлетворяет следующему свойству: если красить вершины, отмеченные литералами, в цвета 0 или 1, а вершины, отмеченные отрицаниями литералов, — в противоположные цвета 1 или 0, то правильная раскраска остальных вершин этого графа в 3 цвета существует (и единственна!) тогда и только тогда, когда хотя бы одно из значений литералов отлично от 0.
Поэтому правильные 3-раскраски построенного графа, для которых вершины  ,
,  ,
,  покрашены в цвета
покрашены в цвета  ,
,  ,
,  соответственно, находятся во взаимно однозначном соответствии с выполняющими наборами значений переменных исходной 3-КНФ.
соответственно, находятся во взаимно однозначном соответствии с выполняющими наборами значений переменных исходной 3-КНФ.
2.7 Данная задача содержит ограничения разного вида, бороться с которыми удобнее по отдельности. Поэтому мы сформулируем промежуточную задачу и построим цепочку полиномиальных сводимостей задач.
Итак, назовем данную задачу ("restricted puzzle"). Задача ("unrestricted puzzle") получается, если отказаться от ограничения на число типов квадратиков и требовать сложить прямоугольник заданных размеров, причем не из всего набора квадратиков, а из некоторого его подмножества.
Опишем неформально цепочку сводимостей
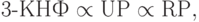
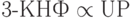 . Для описания этой сводимости будем считать квадратики роботами, которые могут получать и передавать сообщения через стороны. Пара букв допустима, если одна из них означает передачу сообщения, а вторая — прием того же сообщения.
. Для описания этой сводимости будем считать квадратики роботами, которые могут получать и передавать сообщения через стороны. Пара букв допустима, если одна из них означает передачу сообщения, а вторая — прием того же сообщения.
Итак, пусть есть 3-КНФ, множество переменных которой обозначим через  , а множество дизъюнкций — через
, а множество дизъюнкций — через  . Через
. Через 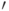 обозначим множество выполнимых дизъюнкций, получаемых из
обозначим множество выполнимых дизъюнкций, получаемых из  подстановкой значений некоторых переменных.
подстановкой значений некоторых переменных.
Будем теперь описывать множество квадратиков и их типы, из которых нужно будет складывать прямоугольник размера  . Одна сторона этого прямоугольника (для определенности — левая) соответствует переменным КНФ, а другая (нижняя) — дизъюнкциям. Роботы-квадратики получают слева сообщения "
. Одна сторона этого прямоугольника (для определенности — левая) соответствует переменным КНФ, а другая (нижняя) — дизъюнкциям. Роботы-квадратики получают слева сообщения " 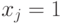 " или "
" или "  ",
",  ; передают вправо то же самое сообщение; получают снизу дизъюнкцию из
; передают вправо то же самое сообщение; получают снизу дизъюнкцию из 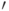 ; подставляют в нее, если возможно, переменную
; подставляют в нее, если возможно, переменную 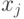 и передают полученную дизъюнкцию вверх, если не получено нулевое значение (другими словами, отсутствуют типы, получающие слева сообщения вида "
и передают полученную дизъюнкцию вверх, если не получено нулевое значение (другими словами, отсутствуют типы, получающие слева сообщения вида "  ", а снизу — "
", а снизу — " 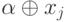 "). Все эти типы не содержат граничных букв. А есть еще 4 угловых типа, двум сторонам которых разрешено выходить на границу, и
"). Все эти типы не содержат граничных букв. А есть еще 4 угловых типа, двум сторонам которых разрешено выходить на границу, и  граничных типов (одна сторона может выходить на границу), которые нумеруются переменными и дизъюнкциями соответственно. Буквы, написанные на сторонах квадратиков граничных типов, обеспечивают однозначную сборку контура прямоугольника. Квадратик каждого типа один. А всего типов
граничных типов (одна сторона может выходить на границу), которые нумеруются переменными и дизъюнкциями соответственно. Буквы, написанные на сторонах квадратиков граничных типов, обеспечивают однозначную сборку контура прямоугольника. Квадратик каждого типа один. А всего типов 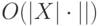 .
.
Таким образом, выполнимость КНФ эквивалентна возможности сложить прямоугольник размера 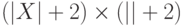 из описанного выше набора типов квадратиков.
из описанного выше набора типов квадратиков.
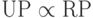 . Пусть есть множество квадратиков, принадлежащих множеству типов
. Пусть есть множество квадратиков, принадлежащих множеству типов  , каждого типа
, каждого типа  по
по 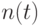 штук (
штук ( 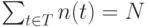 ), из которых нужно сложить прямоугольник
), из которых нужно сложить прямоугольник  . Без ограничения общности можно считать, что
. Без ограничения общности можно считать, что  . Добавим квадратиков: по 2 штуки из
. Добавим квадратиков: по 2 штуки из  дополнительных типов
дополнительных типов 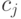 и
и 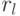 , чтобы выложить внешний контур прямоугольника
, чтобы выложить внешний контур прямоугольника  ,
,  квадратиков еще одного типа
квадратиков еще одного типа  , чтобы можно было использовать квадратики, не вошедшие в прямоугольник, и
, чтобы можно было использовать квадратики, не вошедшие в прямоугольник, и 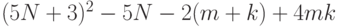 квадратиков типа
квадратиков типа  для получения квадрата. Поскольку
для получения квадрата. Поскольку  , ограничение числа типов длиной стороны квадрата будет выполнено.
, ограничение числа типов длиной стороны квадрата будет выполнено.
Сформулированные условия прямо переводятся на язык букв и их сочетаний. На сторонах квадратиков типа  написана одна и та же буква
написана одна и та же буква  , которая может соседствовать только сама с собой; на одной стороне квадратика типа
, которая может соседствовать только сама с собой; на одной стороне квадратика типа  написана буква
написана буква  , которая может соседствовать со всеми буквами, а на остальных —
, которая может соседствовать со всеми буквами, а на остальных —  ; наконец, на одной стороне квадратиков типов
; наконец, на одной стороне квадратиков типов 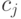 и
и 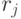 написана буква
написана буква  , а на остальных сторонах написаны буквы, обеспечивающие сборку контура прямоугольника
, а на остальных сторонах написаны буквы, обеспечивающие сборку контура прямоугольника  .
.
Таким образом, чтобы собрать квадрат  из нового набора квадратиков
из нового набора квадратиков  , необходимо и достаточно уметь собирать прямоугольник
, необходимо и достаточно уметь собирать прямоугольник  из некоторого подмножества исходного набора.
из некоторого подмножества исходного набора.
2.8. Поскольку умножение чисел можно произвести за полиномиальное время, Мерлин может сообщить Артуру любое разложение числа  на два множителя.
на два множителя.
2.9 Докажем принадлежность задачи ПРОСТОТА ЧИСЛА классу NP, построив для решения этой задачи недетерминированную машину Тьюринга  , которая рекурсивно вызывает саму себя.
, которая рекурсивно вызывает саму себя.
На вход машине  подается двоичная запись числа
подается двоичная запись числа  , простоту которого нужно проверить. Машина недетерминированно дописывает первообразный корень
, простоту которого нужно проверить. Машина недетерминированно дописывает первообразный корень  по модулю
по модулю  и разложение на простые множители числа
и разложение на простые множители числа  , т.е. такие числа
, т.е. такие числа 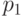 ,
,  ,
, 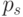 ,
, 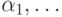 ,
, 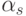 , что
, что
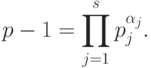 |
( *) |
 (на это хватит времени
(на это хватит времени 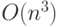 , где
, где  , даже если умножать большие числа в "столбик"), проверяет равенство
, даже если умножать большие числа в "столбик"), проверяет равенство 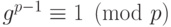 и все неравенства
и все неравенства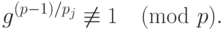
Для этих проверок потребуется время 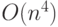 , так как
, так как 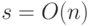 , а возведение в степень
, а возведение в степень  требует
требует 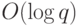 умножений. Далее машина проверяет простоту всех
умножений. Далее машина проверяет простоту всех 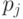 , рекурсивно вызывая саму себя.
, рекурсивно вызывая саму себя.
Описанные выше проверки гарантируют, что порядок числа  в группе
в группе 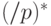 равен
равен  , что эквивалентно простоте
, что эквивалентно простоте  .
.
Оценим теперь время работы такой НМТ на входе длины  . Оно складывается из времени, затрачиваемого на детерминированные действия, и времени, затрачиваемого на недетерминированные действия. Как следует из приведенных выше оценок, количество детерминированных действий ограничено полиномом от длины записей всех чисел, проверяемых на простоту за время работы. Длина записей первообразных корней и кратностей также ограничена полиномом (и даже линейно) от длины записей всех чисел, проверяемых на простоту.
. Оно складывается из времени, затрачиваемого на детерминированные действия, и времени, затрачиваемого на недетерминированные действия. Как следует из приведенных выше оценок, количество детерминированных действий ограничено полиномом от длины записей всех чисел, проверяемых на простоту за время работы. Длина записей первообразных корней и кратностей также ограничена полиномом (и даже линейно) от длины записей всех чисел, проверяемых на простоту.
Таким образом, осталось оценить длину записей чисел, проверяемых на простоту. Если взять произведение всех чисел, проверяемых на простоту на  -м уровне рекурсии, то оно заведомо меньше исходного числа
-м уровне рекурсии, то оно заведомо меньше исходного числа  . Поэтому суммарная длина записей этих чисел не более чем вдвое превышает длину записи
. Поэтому суммарная длина записей этих чисел не более чем вдвое превышает длину записи  (длина записи произведения двух чисел разве что на 1 меньше суммы длин сомножителей). Максимальное из чисел, проверяемых на простоту на
(длина записи произведения двух чисел разве что на 1 меньше суммы длин сомножителей). Максимальное из чисел, проверяемых на простоту на  -м уровне рекурсии, по крайней мере вдвое меньше, чем максимальное из чисел, проверяемых на
-м уровне рекурсии, по крайней мере вдвое меньше, чем максимальное из чисел, проверяемых на  -м уровне. Поэтому максимальный уровень рекурсии не превосходит
-м уровне. Поэтому максимальный уровень рекурсии не превосходит  . Следовательно, общая длина записей всех чисел, проверяемых на простоту при входе
. Следовательно, общая длина записей всех чисел, проверяемых на простоту при входе  , равна
, равна  .
.
Из раздела 4
4.1 Заметим прежде всего, что  заведомо не меньше длины входа в силу иcпользуемых определений2Бывают и другие определения. Так, например, класс log-SPACE определяется с помощью двухленточных машин, у которых на одной ленте записан вход и с нее можно только читать, а на второй ленте используется память
заведомо не меньше длины входа в силу иcпользуемых определений2Бывают и другие определения. Так, например, класс log-SPACE определяется с помощью двухленточных машин, у которых на одной ленте записан вход и с нее можно только читать, а на второй ленте используется память  .
.
.
.
Предположим, что доказана верхняя оценка вида 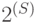 на время работы недетерминированной машины. Тогда можно дословно повторить доказательство теоремы 4.2, построить игру длины
на время работы недетерминированной машины. Тогда можно дословно повторить доказательство теоремы 4.2, построить игру длины  , и вычислить ее результат детерминированной машиной на памяти
, и вычислить ее результат детерминированной машиной на памяти  .
.
Пусть есть НМТ, работающая на памяти  . В процессе работы она может находиться не более чем в
. В процессе работы она может находиться не более чем в 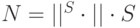 состояниях, где
состояниях, где 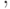 — множество состояний управляющего устройства и внешний алфавит, соответственно. Хотя у НМТ может быть несколько вариантов перехода из данного состояния, из последовательности переходов всегда можно выбросить циклы (ни к чему делать вначале неправильный переход, а затем, вернувшись в то же состояние, — правильный). Так что время работы НМТ ограничено
— множество состояний управляющего устройства и внешний алфавит, соответственно. Хотя у НМТ может быть несколько вариантов перехода из данного состояния, из последовательности переходов всегда можно выбросить циклы (ни к чему делать вначале неправильный переход, а затем, вернувшись в то же состояние, — правильный). Так что время работы НМТ ограничено 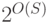 , как и для детерминированной МТ.
, как и для детерминированной МТ.
4.2 Легко сообразить, как имитировать оракул  из
из 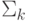 , имея возможность заказывать оракул из
, имея возможность заказывать оракул из 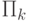 . Нужно заказать оракул
. Нужно заказать оракул 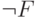 , а дальше брать отрицание от каждого результата его работы.
, а дальше брать отрицание от каждого результата его работы.
Класс 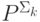 , как и
, как и 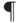 , замкнут относительно взятия дополнений. Так что осталось доказать включение
, замкнут относительно взятия дополнений. Так что осталось доказать включение 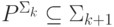 . Это удобно делать, используя игровое определение классов
. Это удобно делать, используя игровое определение классов 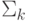 .
.
Пусть есть предикат 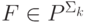 , а вычисляющий его полиномиальный алгоритм использует оракул
, а вычисляющий его полиномиальный алгоритм использует оракул 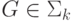 . Игру, которая задает
. Игру, которая задает 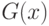 , обозначим
, обозначим  . Опишем теперь игру
. Опишем теперь игру  , выигрыш белых в которой (точнее, наличие выигрышной стратегии) эквивалентен
, выигрыш белых в которой (точнее, наличие выигрышной стратегии) эквивалентен 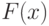 .
.
Первый ход белых в этой игре состоит в объявлении последовательности пар 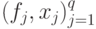 . Белые утверждают, что эта последовательность есть протокол обращений к оракулу в процессе работы алгоритма с оракулом
. Белые утверждают, что эта последовательность есть протокол обращений к оракулу в процессе работы алгоритма с оракулом  , вычисляющего
, вычисляющего 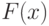 . Более точно это означает, что алгоритм обращается к оракулу
. Более точно это означает, что алгоритм обращается к оракулу  раз,
раз,  -й запрос делается о слове
-й запрос делается о слове 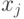 , оракул отвечает на это запрос
, оракул отвечает на это запрос 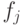 , и окончательный результат
, и окончательный результат 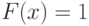 . Следующим ходом черные объявляют индекс
. Следующим ходом черные объявляют индекс  и, если
и, если  , то дополнительно первый ход белых в игре
, то дополнительно первый ход белых в игре 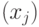 . Далее, если
. Далее, если  , то разыгрывается игра
, то разыгрывается игра 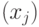 , а если
, а если  , то разыгрывается игра
, то разыгрывается игра 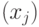 со сдвигом "на темп":
со сдвигом "на темп":  -й ход белых в
-й ход белых в  в этом случае соответствует
в этом случае соответствует  -у ходу черных в
-у ходу черных в 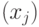 , а
, а  -й ход черных —
-й ход черных —  -у ходу белых в
-у ходу белых в 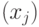 ,
, 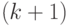 -й ход черных на результат влияния не оказывает.
-й ход черных на результат влияния не оказывает.
Белые выигрывают в этой игре, если 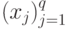 — правильная последовательность аргументов при обращениях к оракулу, результат игры
— правильная последовательность аргументов при обращениях к оракулу, результат игры 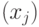 совпадает с
совпадает с 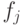 , а результат работы алгоритма для вычисления
, а результат работы алгоритма для вычисления  на входе
на входе  с ответами оракула
с ответами оракула 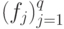 равен 1.
равен 1.
Достаточно ясно, что если 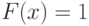 , то у белых есть выигрышная стратегия в
, то у белых есть выигрышная стратегия в  : первым ходом сказать правду, а дальше играть в
: первым ходом сказать правду, а дальше играть в 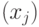 по стратегиям, существование которых вытекает из равенства
по стратегиям, существование которых вытекает из равенства  . Если же
. Если же 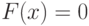 , то в каком-то члене
, то в каком-то члене 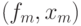 последовательности
последовательности 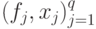 белые должны отклониться от истины. Черные своим ходом должны объявить
белые должны отклониться от истины. Черные своим ходом должны объявить  (и, дополнительно, первый ход за белых в игре
(и, дополнительно, первый ход за белых в игре  при необходимости), дальнейшая их стратегия состоит в том, чтобы доказывать
при необходимости), дальнейшая их стратегия состоит в том, чтобы доказывать 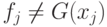 , пользуясь соответствующими стратегиями для
, пользуясь соответствующими стратегиями для 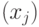 .
.
Из раздела 6
6.1. Поскольку конъюнкция и отрицание образуют полный базис для обычных схем, из лемм 6.1, 6.2 следует, что достаточно реализовать функции 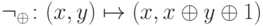 и
и  . Заметим, что
. Заметим, что ![\neg_\oplus[1,2]\double=\neg[2]\qxor[1,2]](/sites/default/files/tex_cache/945662a424dedea358106f4133ccb558.png) , поэтому достаточно реализовать
, поэтому достаточно реализовать  . Для этого заведем вспомогательный бит
. Для этого заведем вспомогательный бит  , содержащий константу 1 (для этого в самом начале и в самом конце применяем
, содержащий константу 1 (для этого в самом начале и в самом конце применяем ![\neg[u]](/sites/default/files/tex_cache/5a6bd2355a390f216554a6adf6bf8c4d.png) ). Тогда
). Тогда ![\qxor\:[1,2]=\wedge_\oplus[u,1,2]](/sites/default/files/tex_cache/b6d2c132a28b7bfec0e30671e0fc8b75.png) .
.

