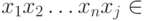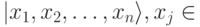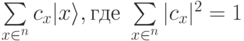Квантовые вычисления
Как уже говорилось во введении, обычные компьютеры не используют всех возможностей, предоставляемых природой. В них выполняются преобразования на конечных множествах состояний (действия с 0 и 1), а в природе есть возможность делать унитарные преобразования, т.е. действовать на бесконечном множестве1Конечно, настоящей бесконечности в природе не бывает. В данном случае дело в том, что унитарное преобразование можно задать лишь с некоторой точностью - подробности см. в "лекции 7" . Эта возможность описывается квантовой механикой. Устройства (реальные или воображаемые), использующие эту возможность, называются квантовыми компьютерами.
Заранее неясно, увеличиваются ли вычислительные возможности при переходе от преобразований конечных множеств к унитарным преобразованиям конечномерных пространств. Сейчас есть основания полагать, что такое увеличение действительно происходит. В качестве примера можно привести задачу о разложении числа на множители: для обычных компьютеров неизвестны полиномиальные алгоритмы ее решения, а для квантовых компьютеров такие алгоритмы есть.
Обычный компьютер работает с состояниями из конечного числа битов. Каждый бит может находиться в одном из двух состояний 0 или 1. Состояние всей системы задается указанием значений всех битов. Поэтому множество состояний 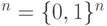 конечно и имеет мощность
конечно и имеет мощность 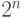 .
.
Квантовый компьютер работает с конечными наборами элементарных состояний, называемых q-битами. Каждый q-бит имеет два выделенных состояния (если считать q-биты спинами, то это состояния "спин вверх" и "спин вниз"). Указание выделенных состояний для каждого q-бита системы задает не все возможные состояния системы, а только базисные. Возможны также любые линейные комбинации базисных состояний с комплексными коэффициентами. Базисные состояния мы будем обозначать 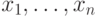 , где
, где  , или
, или 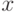 , где
, где 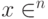 . Произвольное состояние системы может быть представлено в виде2Скобки
. Произвольное состояние системы может быть представлено в виде2Скобки  в записи
в записи  не обозначают никакой операции над объектом
не обозначают никакой операции над объектом  — они просто указывают на то, что
— они просто указывают на то, что  является вектором.
является вектором.
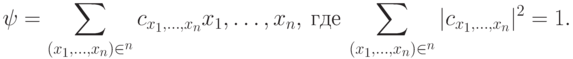
Пространство состояний для такой системы — конечномерное (размерности 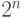 ) пространство над полем комплексных чисел.
) пространство над полем комплексных чисел.
Небольшое уточнение: если умножить вектор 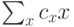 на фазовый множитель,
на фазовый множитель, 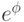 , (
, (  — вещественное), то получится физически неотличимое состояние. Таким образом, состояние квантового компьютера — это вектор единичной длины, заданный с точностью до фазового множителя.
— вещественное), то получится физически неотличимое состояние. Таким образом, состояние квантового компьютера — это вектор единичной длины, заданный с точностью до фазового множителя.
Вычисление можно представлять как последовательность преобразований на множестве состояний системы. Опишем, какие преобразования возможны в классическом, а какие — в квантовом случае.
| Классический случай: | Квантовый случай: |
|---|---|
преобразования — это функции из  в в 
|
преобразования — это унитарные операторы, то есть операторы, сохраняющие длину вектора  . . |
Замечание. Все сказанное относится только к замкнутым системам. Реальный квантовый компьютер — это часть большой системы (Вселенной), взаимодействующая с остальным миром. Квантовые состояния и преобразования открытых систем будут рассмотрены в разделах 9-10.
Теперь нужно дать формальное определение квантового вычисления. Как и в классическом случае, можно определить квантовые машины Тьюринга или квантовые схемы. Мы выбираем второй подход, который удобнее по ряду причин.

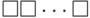 биты
биты