Квантовые вычисления
Определения и обозначения
Пространство состояний системы из  q-битов
q-битов 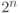 можно записать в виде тензорного произведения
можно записать в виде тензорного произведения 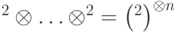 . Сомножители соответствуют пространству состояний одного q-бита.
. Сомножители соответствуют пространству состояний одного q-бита.
Тензорное произведение двух пространств  и
и  , в которых фиксированы базисы
, в которых фиксированы базисы 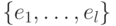 и
и 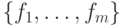 , можно определить как пространство с базисом из элементов
, можно определить как пространство с базисом из элементов  . (В данном случае
. (В данном случае  — это то же самое, что
— это то же самое, что 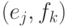 , т.е. просто пара векторов.) Размерность тензорного произведения равна
, т.е. просто пара векторов.) Размерность тензорного произведения равна 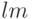 (произведению размерностей сомножителей).
(произведению размерностей сомножителей).
Такое определение неинвариантно, т.е. зависит от выбора базисов в перемножаемых пространствах. Можно дать инвариантное определение. Для этого рассмотрим вначале пространство (бесконечномерное) с базисом  , где
, где 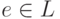 ,
, 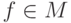 — произвольные векторы из перемножаемых пространств. Тензорное произведение будет факторпространством этого пространства по подпространству, порожденному векторами вида
— произвольные векторы из перемножаемых пространств. Тензорное произведение будет факторпространством этого пространства по подпространству, порожденному векторами вида
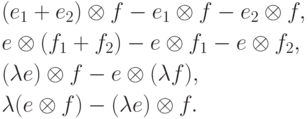
Можно доказать, что данные определения эквивалентны.
В нашем случае имеется естественный выделенный базис (соответствующий выделенным состояниям): для 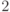 —
— 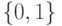 , а для
, а для 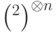 —
— 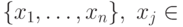 . Пространство
. Пространство 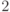 с выделенным базисом обозначается через
с выделенным базисом обозначается через  . Выделенный базис считается ортонормированным, это задает скалярное произведение на пространстве состояний. Коэффициенты
. Выделенный базис считается ортонормированным, это задает скалярное произведение на пространстве состояний. Коэффициенты 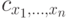 разложения вектора
разложения вектора 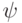 по этому базису называются амплитудами. Их физический смысл состоит в том, что квадрат модуля амплитуды
по этому базису называются амплитудами. Их физический смысл состоит в том, что квадрат модуля амплитуды 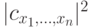 интерпретируется как вероятность обнаружить систему в данном базисном состоянии. Как и должно быть, суммарная вероятность всех состояний равна
интерпретируется как вероятность обнаружить систему в данном базисном состоянии. Как и должно быть, суммарная вероятность всех состояний равна  , поскольку длина вектора предполагается единичной. (Вероятности будут подробно обсуждаться позже; до некоторых пор мы будем заниматься линейной алгеброй — изучать унитарные операторы на пространстве
, поскольку длина вектора предполагается единичной. (Вероятности будут подробно обсуждаться позже; до некоторых пор мы будем заниматься линейной алгеброй — изучать унитарные операторы на пространстве 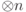 ).
).
Мы будем использовать (и уже использовали) принятые в физике обозначения, относящиеся к векторам и скалярному произведению в гильбертовом пространстве (их ввел Дирак). Векторы обозначаются 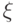 , скалярное произведение —
, скалярное произведение — 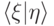 . Если
. Если  и
и 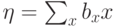 , то
, то  . (Здесь и далее
. (Здесь и далее 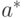 обозначает комплексное сопряжение.) В записи векторов скобки нужны лишь "для красоты" — они указывают на тип объекта и придают симметрию обозначениям (см. ниже). Вместо
обозначает комплексное сопряжение.) В записи векторов скобки нужны лишь "для красоты" — они указывают на тип объекта и придают симметрию обозначениям (см. ниже). Вместо 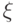 можно было бы написать просто
можно было бы написать просто  , хотя это и не принято. Поэтому
, хотя это и не принято. Поэтому  — и то, и другое обозначает вектор
— и то, и другое обозначает вектор  .
.
Скалярное произведение антилинейно по первому аргументу3Обратите внимание, что математики обычно считают, что скалярное произведение в унитарном пространстве антилинейно по второму аргументу. и линейно по второму, т.е.
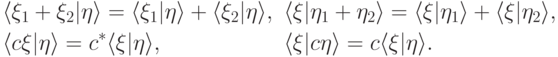
Если в обозначении скалярного произведения взять левую половину, то получим бра-вектор 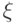 , т.е. линейный функционал на кет-векторах (векторах нашего пространства). Бра- и кет-векторы находятся во взаимно однозначном соответствии. (Тем не менее, нужно их как-то различать — именно для этого и были введены угловые скобки.) Из-за антилинейности скалярного произведения по первому аргументу имеем равенство
, т.е. линейный функционал на кет-векторах (векторах нашего пространства). Бра- и кет-векторы находятся во взаимно однозначном соответствии. (Тем не менее, нужно их как-то различать — именно для этого и были введены угловые скобки.) Из-за антилинейности скалярного произведения по первому аргументу имеем равенство 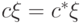 . Бра-вектор можно записать в виде строки, а кет-вектор — в виде столбца (чтобы его можно было умножить слева на матрицу):
. Бра-вектор можно записать в виде строки, а кет-вектор — в виде столбца (чтобы его можно было умножить слева на матрицу):
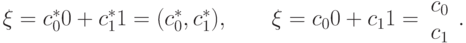
Запись 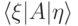 (
(  — линейный оператор) можно толковать двояко: либо как скалярное произведение вектора
— линейный оператор) можно толковать двояко: либо как скалярное произведение вектора 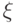 на вектор
на вектор 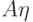 , либо как —
, либо как — 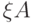 на
на 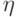 . Так появляется сопряженный оператор
. Так появляется сопряженный оператор 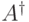 : по определению,
: по определению,  (бра-вектор, соответствующий
(бра-вектор, соответствующий  ) равен линейному функционалу
) равен линейному функционалу 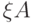 . Из определения сразу следует, что
. Из определения сразу следует, что
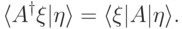
Унитарный оператор — это линейный оператор, сохраняющий скалярное произведение. Условие

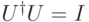 (где
(где  — тождественный оператор).
— тождественный оператор).Наше определение скалярного произведения в 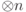 согласовано с тензорным произведением:
согласовано с тензорным произведением:
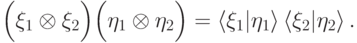
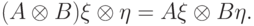
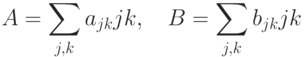
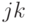 — линейный оператор:
— линейный оператор: 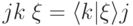 ), то матричные элементы оператора
), то матричные элементы оператора 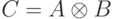 имеют вид
имеют вид 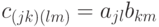 .
.Вычисление состоит из преобразований, считаемых элементарными (выполняемых за единицу времени).
Элементарное преобразование в классическом случае: такая функция из  в в  , которая зависит от небольшого (не зависящего от , которая зависит от небольшого (не зависящего от  ) числа битов и изменяет также небольшое число битов. ) числа битов и изменяет также небольшое число битов. |
Элементарное преобразование в квантовом случае: тензорное произведение произвольного унитарного оператора, действующего на части сомножителей 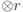 , где , где  мало ( мало ( 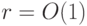 ), и тождественного оператора, действующего на остальных сомножителях. ), и тождественного оператора, действующего на остальных сомножителях. |
Тензорное произведение некоторого оператора  , действующего на множестве q-битов
, действующего на множестве q-битов  , и тождественного оператора, действующего на остальных q-битах, будем обозначать
, и тождественного оператора, действующего на остальных q-битах, будем обозначать ![U[A]](/sites/default/files/tex_cache/9f8f36987373f5f08d8a3aaaa85a8875.png) . (В частности,
. (В частности, ![U[1,\dots,r]\double=U\otimes I](/sites/default/files/tex_cache/abd459a28d72cd33922d2a0fe651fe4d.png) обозначает действие на первых
обозначает действие на первых  q-битах.)
q-битах.)
