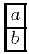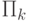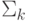Предисловие
В последние годы интерес к тому, что называется "квантовые компьютеры", необычайно возрос. Идея использования возможностей квантовой механики при организации вычислений выглядит все более привлекательной, начаты экспериментальные работы в этой области.
Однако перспективы физической реализации квантовых компьютеров пока совершенно неясны. Скорее всего, это дело нескольких десятилетий. Основные достижения в этой области носят пока чисто математический характер.
Эта книга предназначена для первоначального знакомства с математической теорией квантовых вычислений. Для удобства читателя вначале дается краткое введение в классическую теорию сложности вычислений. Затем подробно излагаются основы теории квантовых вычислений, включая описание основных известных к настоящему времени эффективных квантовых алгоритмов.
Основу книги составили материалы курса "Классическое и квантовое вычисление", прочитанного А. Шенем (классические вычисления) и А. Китаевым (квантовые вычисления) в Высшем колледже математики Независимого Московского университета в весеннем семестре 1998 г. При подготовке книги также использовались материалы курса Physics 229 - Advanced Mathematical Methods of Physics (Quantum computation), который вели Дж. Прескилл (John Preskill) и А. Китаев (при участии А. Ландала (Andrew Landahl)) в Калифорнийском технологическом институте в 1998-1999 уч. г.
Необходимые для чтения этой книги знания невелики. В сущности, достаточно знания линейной алгебры в объеме стандартного университетского курса, элементарной теории вероятностей, элементарной теории чисел и минимальных представлений о теории алгоритмов (например, иметь навыки практического программирования нетривиальных алгоритмов).
Обозначения
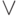 |
дизъюнкция (логическое ИЛИ) |
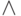 |
конъюнкция (логическое И) |
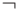 |
отрицание |
 |
сложение по модулю 2 (а также прямая сумма линейных пространств) |
 |
импликация (логическое следование) |
 |
логическая эквивалентность |
 |
множество конечных слов в алфавите 
|
 |
пустой символ (пробел) в алфавите машины Тьюринга |
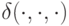 |
функция переходов машины Тьюринга |
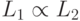 |
сводимость предикатов по Карпу ( 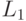 сводится к сводится к 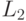 ) (
"Класс NP: сводимость и полнота"
) ) (
"Класс NP: сводимость и полнота"
) |
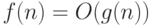 |
существует такое число  , что , что 
|
 |
существует такое число  , что , что 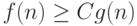
|
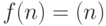 |
то же самое, что 
|
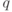 |
конечное поле из  элементов элементов |
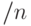 |
кольцо вычетов по модулю 
|
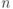 |
аддитивная группа кольца 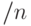
|
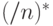 |
мультипликативная группа обратимых элементов 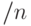
|
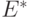 |
( 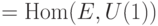 ) — группа характеров абелевой группы ) — группа характеров абелевой группы 
|
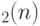 |
симплектическая группа над полем 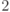 размерности размерности  (
"Классические и квантовые коды"
) (
"Классические и квантовые коды"
) |
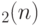 |
расширенная симплектическая группа над полем 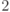 размерности размерности  (
"Классические и квантовые коды"
) (
"Классические и квантовые коды"
) |
 |
множество комплексных чисел |
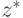 |
комплексное сопряжение |
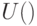 |
группа унитарных операторов на пространстве 
|
 |
специальная унитарная группа на пространстве 
|
 |
специальная ортогональная группа на евклидовом пространстве 
|
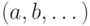 |
пространство, порожденное векторами 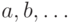
|
 |
пространство линейных функционалов на пространстве 
|
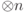 |
 -я тензорная степень -я тензорная степень |
 |
пространство линейных операторов на 
|
 |
пространство линейных отображений из  в
в 
|
 |
классический бит (множество 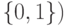
|
 |
квантовый бит (q-бит, пространство 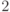 ) ) |
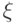 |
бра-вектор ( "Квантовые вычисления" ) |
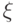 |
кет-вектор ( "Квантовые вычисления" ) |
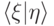 |
скалярное произведение |
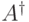 |
эрмитово сопряженный оператор |
 |
обратимое копирование бита (Controlled NOT) ( "Соотношение между классическим и квантовым вычислением" ) |
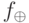 |
обратимая функция, соответствующая булевой функции  (
"Соотношение между классическим и квантовым вычислением"
) (
"Соотношение между классическим и квантовым вычислением"
) |
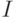 |
тождественный оператор на пространстве 
|
 |
унитарный оператор, соответствующий перестановке  (
"Соотношение между классическим и квантовым вычислением"
) (
"Соотношение между классическим и квантовым вычислением"
) |
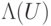 |
оператор  с квантовым управлением (
"Базисы для квантовых схем"
) с квантовым управлением (
"Базисы для квантовых схем"
) |
 |
проектор (оператор проектирования) на подпространство 
|
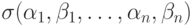 |
базисные операторы на пространстве 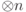 (
"Классические и квантовые коды"
) (
"Классические и квантовые коды"
) |
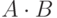 |
преобразование матриц плотности 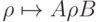 (
"Классические и квантовые коды"
) (
"Классические и квантовые коды"
) |
![U[A]](/sites/default/files/tex_cache/9f8f36987373f5f08d8a3aaaa85a8875.png) |
оператор, действующий на квантовый регистр (множество q-битов)  (
"Квантовые вычисления"
) (
"Квантовые вычисления"
) |
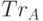 |
частичный след от оператора  по пространству по пространству  (
"Квантовые вероятности"
) (
"Квантовые вероятности"
) |
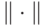 |
норма вектора ( "Базисы для квантовых схем" ) или операторная норма оператора ( "Соотношение между классическим и квантовым вычислением" ) |
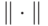 |
следовая норма ( "Классические и квантовые коды" ) |
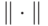 |
норма для преобразований матриц плотности ( "Классические и квантовые коды" ) |
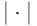 |
мощность множества или модуль числа |
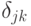 |
символ Кронекера |
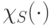 |
характеристическая функция множества 
|
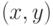 |
наибольший общий делитель  и и 
|
 |
сравнение по модулю 
|
 |
остаток по модулю 
|
представление рационального числа 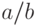 в виде несократимой дроби в виде несократимой дроби |
|
![\Prob[A]](/sites/default/files/tex_cache/afcda03a6fd0aa829f211dce1d7e7cdf.png) |
вероятность события 
|
 |
условная вероятность (в различных контекстах) |
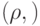 |
квантовая вероятность ( "Квантовые вероятности" ) |
Обозначения матриц:
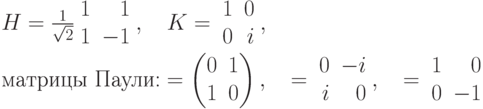
Обозначения сложностных классов: