Классические и квантовые вычисления
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 616 / 27 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист
Теги: beta, BPP, NP, алгоритмы, алфавит, базис, вычисления, вычислимость, дизъюнкция, игры, квантовые вычисления, КНФ, машина Тьюринга, подгруппа, сложность, собственное число, теория, теория чисел, управляющее устройство, элементы, эффективность
Лекция 10:

Физически реализуемые преобразования матриц плотности
A
|
версия для печати
< Лекция 9 || Лекция 10: 123 || Лекция 11 >
Аннотация: В лекции рассматриваются основные преобразования матриц плотности, описан механизм измерения квантовых регистров, вводится понятие детерминированного измерения, приводится задача "о квантовой телепортации".
Ключевые слова: скалярное произведение, интерпретация, вероятность, равенство, тождество, базис, условная вероятность, пространство состояний

Теперь опишем, какие преобразования матриц плотности допустимы с физической точки зрения.

  1. Унитарный оператор переводит матрицу плотности чистого состояния 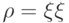\rho=\ket\xi\bra\xi в матрицу \rho'=U\ket\xi\bra\xi U^\dagger. Естественно считать (по линейности), что такой же формулой задается и действие унитарного оператора на произвольные матрицы плотности:
    \rho\stackrel{\scriptscriptstyle U}{\mapsto} U\rho U^\dagger.
  2. Второй тип преобразования состоит во взятии частичного следа. Если есть \rho\in\LL(\calN\otimes\calF), то отбрасывание второй системы задается преобразованием
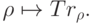
    \rho\mapsto Tr_\calF \rho.
  3. Вспомним, что нам еще бывает нужно брать напрокат q-биты в состоянии 0. Пусть есть состояние 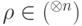\rho\in\LL(\BB^{\otimes n}). Рассмотрим изометрическое (сохраняющее скалярные произведения) вложение V\colon \BB^{\otimes n} \double\to \BB^{\otimes N} в пространство большей размерности, задаваемое формулой \ket\xi\stackrel{\scriptscriptstyle V}{\mapsto} \ket\xi\otimes\ket{0^{N-n}}. Матрица плотности \rho при этом преобразуются в \rho\otimes\ket{0^{N-n}}\bra{0^{N-n}}. Для любого изометрического вложения V по аналогии полагаем
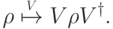
    \rho\stackrel{\scriptscriptstyle V}{\mapsto} V\rho V^\dagger.

Будем считать, что физически реализуемые преобразования матриц плотности есть в точности композиции любого числа преобразований типа 2 и 3 (случай 1 — частный случай преобразования типа 3).

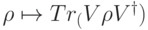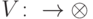Задача 10.1. Докажите, что любое физически реализуемое преобразование матриц плотности имеет вид \rho\mapsto Tr_\calF(V\rho V^\dagger), где V\colon\calN\double\to \calN\otimes\calF — изометрическое вложение.


Операция взятия частичного следа означает забывание (отбрасывание) одной из подсистем. Покажем, что такая интерпретация является разумной, а именно, дальнейшая судьба отброшенной системы не влияет на величины, характеризующие оставшуюся систему. Возьмем систему, состоящую из двух подсистем и находящуюся в некотором состоянии \rho\in\LL(\calN\otimes\calF). Если мы выбрасываем вторую систему (в мусорную корзину), то она будет подвергаться неконтролируемым воздействиям. Пусть мы применили какой-то оператор U к первой системе. 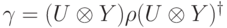Получили состояние \gamma=(U\otimes Y)\rho(U\otimes Y)^\dagger, где Y — произвольный унитарный оператор (действие мусорной корзины на мусор). 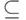Если мы хотим найти вероятность для подпространства \calM\subseteq\calN, относящегося к первой системе (мусор нас не интересует), то она не зависит от Y и равна

\PP(\gamma,\calM\otimes\calF)=\PP( Tr_\calF\gamma, \calM)\,=\, \PP\left(U( Tr_\calF\rho)U^\dagger,\calM\right).
Здесь первое равенство — это свойство 4q квантовой вероятности, а второе равенство — новое свойство:
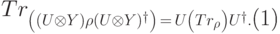\begin{equation}\label{част-след-упр} Tr_\calF\left((U\otimes Y)\rho(U\otimes Y)^\dagger\right)\, =\, U\left(Tr_\calF\rho\right)U^\dagger. \end{equation} ( 10.1)

Задача 10.2. Докажите тождество (10.1) для частичного следа.

Задача 10.3. Запишем линейный оператор T\colon\LL(\calN)\to\LL(\calM) в координатном виде:

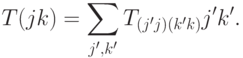
T(\ket{j}\bra{k})=\sum_{j',k'} T_{(j'j)(k'k)} \ket{j'}\bra{k'}.
Докажите, что физическая реализуемость T эквивалентна набору из трех условий:

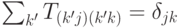  1. \sum_{k'} T_{(k'j)(k'k)}=\delta_{jk} (символ Кронекера);
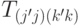  2. T_{(j'j)(k'k)}^*=T^{\ms}_{(k'k)(j'j)} ;
  3. T_{(j'j)(k'k)} — неотрицательная матрица (по парам индексов).

Задача 10.4. Докажите, что линейный оператор T\colon \LL(\calN)\to\LL(\calM) является физически реализуемым преобразованием матриц плотности тогда и только тогда, когда выполнены три условия:

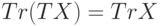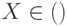  1. Tr(TX)=Tr X для любого X\in\LL(\calN) ;
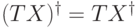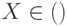  2. (TX)^\dagger=TX^\dagger для любого X\in\LL(\calN) ;
  3. T является вполне положительным преобразованием. А именно, для любого пространства \calG преобразование T\otimes\id_{\LL(\calG)}\colon \LL(\calN\otimes\calG)\double\to\LL(\calM\otimes\calG) отображает неотрицательные операторы в неотрицательные.
Дальше >>
< Лекция 9 || Лекция 10: 123 || Лекция 11 >

Вопросы и ответы

вопросов: 1
Илья Молочков
Илья Молочков
ответить