НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 5: Квантовые вычисления

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 611 / 26 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 10 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

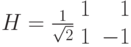Пример 5.1. Приведем матрицу оператора H[2] , действующего в пространстве $\BB^{\otimes3}$ . Оператор $H=\frac{1}{\sqrt2}\leftp\begin{array}{rr} 1&1\\1&-1\end{array}\rightp$ действует на второй q-бит, на остальных q-битах действие тождественное. Базисные векторы расположены в лексикографическом порядке: от 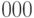$\ket{000}$ до $\ket{111}$ .

$H[2] \,=\, \frac{1}{\sqrt2} \leftp \begin{array}{*8 r} 1& 0& 1& 0& 0& 0& 0& 0\\ 0& 1& 0& 1& 0& 0& 0& 0\\ 1& 0&-1& 0& 0& 0& 0& 0\\ 0& 1& 0&-1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 1& 0\\ 0& 0& 0& 0& 0& 1& 0& 1\\ 0& 0& 0& 0& 1& 0&-1& 0\\ 0& 0& 0& 0& 0& 1& 0&-1 \end{array} \rightp\ .$

С этого места начинается вычислительная сложность. Пусть 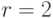r=2 , тогда — некоторая матрица $4\times4$ , $U\otimes I$ — матрица размерности $2^n\times 2^n$ , у которой по диагонали стоят блоки из матриц . Эта матрица представляет один элементарный шаг. Когда применяется несколько таких операторов к разным парам q-битов, результат будет выглядеть гораздо сложнее. Не видно способа определить этот результат, кроме прямого перемножения матриц. Поскольку размеры матриц экспоненциально велики, потребуется экспоненциальное время для их перемножения.

Заметим однако, что вычисление матричных элементов возможно на полиномиально ограниченной памяти. Пусть нужно найти матричный элемент 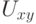$U_{xy}$ оператора

$U = U^{(l)}[j_l,k_l]\, U^{(l-1)}[j_{l-1},k_{l-1}]\cdot\ldots\cdot U^{(2)}[j_2,k_2]\, U^{(1)}[j_1,k_1].$

Очевидно, что

$\left(U^{(l)}\cdot\ldots\cdot U^{(1)}\right)_{x_lx_0}=\sum_{x_{l-1},\dots, x_1}^{} U^{(l)}_{x_lx_{l-1}}\cdot\ldots\cdot U^{(1)}_{x_1x_0}.$

( 5.1)

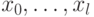(Здесь $x_0,\dots,x_l$ — строки длиной

битов.) Для вычисления этой суммы достаточно (l-1)

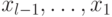-го регистра для хранения текущих значений $x_{l-1}, \dots, x_1$ , еще одного регистра для хранения частичной суммы и некоторого фиксированного количества регистров для вычисления промежуточных произведений.

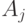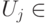Определение 5.1. Квантовая схема. Пусть $\calA$ — некоторое множество унитарных операторов (базис). Тогда квантовая схема в базисе $\calA$ — это последовательность $U_1[A_1],\dots,U_l[A_l]$ , где A_j — множества q-битов, $U_j\in\calA$ .

Оператор, реализуемый квантовой схемой. Это оператор 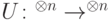$U\colon \BB^{\otimes n}\to \BB^{\otimes n}$ , равный $U_l[A_l]\cdot\ldots\cdot U_1[A_1]$ .

Это определение не очень хорошо, так как не учитывает возможность использования дополнительной памяти в процессе вычисления. Поэтому дадим еще одно определение.

Оператор 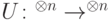$U\colon \BB^{\otimes n}\to \BB^{\otimes n}$ , реализуемый схемой в расширенном смысле. Это такой оператор, что произведение

$W=U_l[A_l]\cdot\ldots\cdot U_1[A_1],$

действующее на

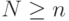q-битов, $N\geq n$ , для любого вектора 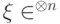$\ket{\xi}\in\BB^{\otimes n}$ удовлетворяет условию $W(\ket\xi\double\otimes\ket{0^{N-n}})=\left(U\ket\xi\right)\otimes\ket{0^{N-n}}$ .

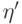Таким образом, мы "берем напрокат" дополнительную память, заполненную нулями, и должны возвратить ее в прежнем состоянии. Какой смысл имеет такое определение? Зачем нужно требовать, чтобы дополнительные q-биты вернулись в состояние $\ket{0^{N-n}}$ ? На самом деле это условие чисто техническое, однако важно, чтобы вектор состояния в конце вычисления был разложим, т.е. имел вид $\ket{\xi'}\otimes\ket{\eta'}$ (с произвольным $\ket{\eta'}$ ). Если это так, то первая подсистема находится в определенном состоянии 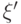$\ket{\xi'}$ , поэтому про вторую подсистему (дополнительную память) можно забыть. В противном случае, совместное состояние двух подсистем оказывается "запутанным" (entangled), поэтому первую подсистему нельзя отделить от второй.

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Квантовые вычисления

Вопросы и ответы