Классические и квантовые коды
Основные определения и простейшие следствия.
Следующее определение дает в квантовом случае формальное выражение требования "различные состояния переходят в различные состояния" (это необходимое условие возможности восстановления исходных состояний физически реализуемым преобразованием).
Определение 14.6. Квантовый код (подпространство 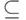 ) исправляет ошибки из
) исправляет ошибки из 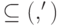 , если
, если
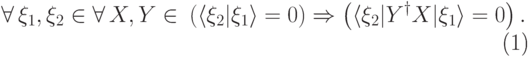 |
( 14.8) |
Определение 14.7. Физически реализуемое преобразование
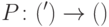
 и пространства ошибок
и пространства ошибок  ), если
), если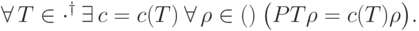
 сохраняет след, то
сохраняет след, то 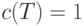 .
.Теорема 14.2. Если код  исправляет ошибки из
исправляет ошибки из  , то исправляющее преобразование существует.
, то исправляющее преобразование существует.
Доказательство будет дано ниже. Обратное утверждение доказано в [4].
Пример 14.4. Тривиальный код типа  : пусть
: пусть  , а
, а ![\calE=\calE[m+1,\dots,n]](/sites/default/files/tex_cache/6fd559d8c9e5435ff3d685d8918d2d47.png) , т.е. для кодирования используются первые
, т.е. для кодирования используются первые  q-битов, а ошибки действуют на остальные q-биты. Условие (14.8), очевидно, выполнено. В качестве исправляющего преобразования можно взять
q-битов, а ошибки действуют на остальные q-биты. Условие (14.8), очевидно, выполнено. В качестве исправляющего преобразования можно взять  , где
, где 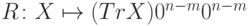 . Преобразование
. Преобразование  реализуется очень просто: выбрасываем последние
реализуется очень просто: выбрасываем последние  q-битов и заменяем их на новые q-биты в состоянии
q-битов и заменяем их на новые q-биты в состоянии  . Практической пользы от такого кода, конечно, мало. Интересно, однако, что любой квантовый код, исправляющий ошибки, в определенном смысле похож на тривиальный (см. лемму 14.3 ниже).
. Практической пользы от такого кода, конечно, мало. Интересно, однако, что любой квантовый код, исправляющий ошибки, в определенном смысле похож на тривиальный (см. лемму 14.3 ниже).
Пример 14.5. Рассмотрим квантовый аналог кода с повторением. Пусть пространство 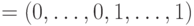 . Рассмотрим два состояния
. Рассмотрим два состояния 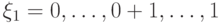 и
и 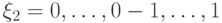 . Ошибку выберем так:
. Ошибку выберем так: 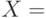 ,
, ![Y=\sz[1]](/sites/default/files/tex_cache/81b996edab4ff1ad2fd91016fec6a654.png) . Очевидно, что
. Очевидно, что  . При этом
. При этом  , что противоречит определению кода, исправляющего ошибки. Мы видим, что код с произвольно большим повторением не защищает даже от одной ошибки.
, что противоречит определению кода, исправляющего ошибки. Мы видим, что код с произвольно большим повторением не защищает даже от одной ошибки.
Ошибки вида ![\sx[1]](/sites/default/files/tex_cache/11644418fe0884dc4513fa566034ee98.png) называются классическими, а ошибки вида
называются классическими, а ошибки вида ![\sz[1]](/sites/default/files/tex_cache/c475a4663cd038376b22f284a25b5734.png) называются фазовыми.
называются фазовыми.
В определении 14.6 речь шла только о парах ортогональных состояний. Давайте посмотрим, что получается на произвольных парах. Зафиксируем 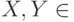 и обозначим
и обозначим 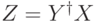 . Оказывается, что
. Оказывается, что
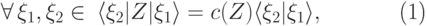 |
( 14.9) |
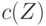 — некоторое комплексное число, не зависящее от
— некоторое комплексное число, не зависящее от 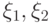 . Действительно, пусть
. Действительно, пусть 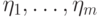 — ортонормированный базис пространства
— ортонормированный базис пространства  . По определению 14.6
. По определению 14.6  при
при 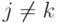 , а
, а  не зависит от
не зависит от  , так как
, так как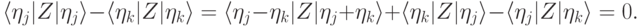
Заметим, что если 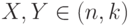 , то
, то 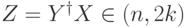 .
.
Определение 14.8. Код  обнаруживает ошибки из
обнаруживает ошибки из 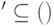 , если
, если
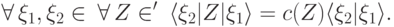
 , при котором код не обнаруживает ошибки из
, при котором код не обнаруживает ошибки из 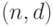 .
.Таким образом, код исправляет  ошибок, если
ошибок, если 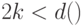 .
.
Теперь мы перейдем к доказательству теоремы 14.2.
Лемма 14.3. Пусть квантовый код 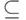 исправляет ошибки из
исправляет ошибки из 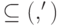 . Тогда существует унитарное пространство
. Тогда существует унитарное пространство  , изометрическое вложение
, изометрическое вложение  и линейное отображение
и линейное отображение 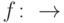 , такие что
, такие что
 |
( 14.10) |
Доказательство. Пусть 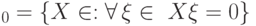 . Рассмотрим фактор-пространство
. Рассмотрим фактор-пространство 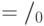 и естественное отображение
и естественное отображение 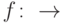 . Линейное отображение
. Линейное отображение  , удовлетворяющее условию (14.10), строится каноническим образом; нужно лишь проверить его изометричность.
, удовлетворяющее условию (14.10), строится каноническим образом; нужно лишь проверить его изометричность.
Скалярное произведение на пространстве  можно задать при помощи функции
можно задать при помощи функции  из свойства кода (14.9): если
из свойства кода (14.9): если 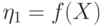 и
и 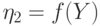 , то
, то  . Очевидно, что эта величина не зависит от выбора
. Очевидно, что эта величина не зависит от выбора  и
и  . Ясно также, что
. Ясно также, что 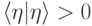 , если
, если  . Формула (14.9) как раз и означает, что отображение
. Формула (14.9) как раз и означает, что отображение  является изометрическим.
является изометрическим.
Доказательство (теоремы 14.2). Представим пространство 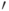 как сумму взаимно ортогональных подпространств:
как сумму взаимно ортогональных подпространств:  , где
, где  — отображение из предыдущей леммы. Пусть
— отображение из предыдущей леммы. Пусть 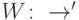 — каноническое вложение, а
— каноническое вложение, а  — произвольное физически реализуемое преобразование. Тогда мы можем определить
— произвольное физически реализуемое преобразование. Тогда мы можем определить
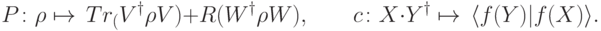
 линейно продолжается на все пространство
линейно продолжается на все пространство 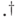 ).
).Лемму 14.3 и доказательство теоремы 14.2 можно неформально изложить таким образом. Код, исправляющий ошибки, характеризуется тем, что ошибка не смешивается с закодированной информацией, т.е. остается в виде отдельного тензорного сомножителя. Исправляющее преобразование извлекает эту "встроенную ошибку" и выбрасывает ее в мусорную корзину.
Задача 14.3. Пусть код  обнаруживает ошибки из
обнаруживает ошибки из  . Докажите, что состояние
. Докажите, что состояние  можно восстановить, не используя q-битов из множества
можно восстановить, не используя q-битов из множества  .
.
