Классические и квантовые коды
Примеры классических кодов.
-
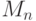 типа
типа 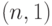 ; для него
; для него 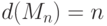 .
.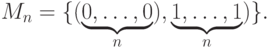
Это самая простая схема кодирования. Повторяем каждый бит много раз, а после каждой операции восстанавливаем кодовое слово, заменяя значения битов на то, которое встречается чаще.
Эта серия кодов, как будет показано ниже, не обобщается на квантовый случай.
- Проверка на четность. Код
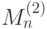 типа
типа 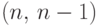 , для него
, для него 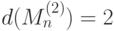 . Состоит из всех четных слов, т.е. слов, содержащих четное число единиц.
. Состоит из всех четных слов, т.е. слов, содержащих четное число единиц. -
Код Хэмминга
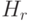 . Это код типа
. Это код типа 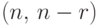 , где число
, где число 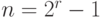 .
.Слова из
 — это последовательности битов
— это последовательности битов 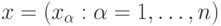 . Номер каждого бита можно записать в двоичной системе как
. Номер каждого бита можно записать в двоичной системе как 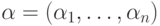 . Введем множество контрольных сумм(суммирование здесь понимается по модулю 2). На рисунке выделены множества битов, входящих в контрольные суммы при
. Введем множество контрольных сумм(суммирование здесь понимается по модулю 2). На рисунке выделены множества битов, входящих в контрольные суммы при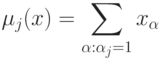
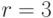 (полезно видеть в этой картинке трехмерный куб).
(полезно видеть в этой картинке трехмерный куб).
Множество слов кода Хэмминга задается условием равенства всех контрольных сумм 0 (т.е. оно является подпространством по модулю 2). Можно показать, что для кода Хэмминга
 .
.
Линейные коды.
Пусть есть множество 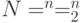 . Линейный код
. Линейный код 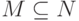 — это линейное подпространство. Линейные коды удобно задавать двойственным базисом (как множество решений системы линейных уравнений).
— это линейное подпространство. Линейные коды удобно задавать двойственным базисом (как множество решений системы линейных уравнений).
Пример 14.2. Код Хэмминга, рассмотренный выше, задается как множество решений системы уравнений
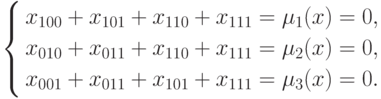
Квантовые коды.
Будем давать определения аналогично классическому случаю. Набору условных вероятностей  соответствует физически реализуемое преобразование матриц плотности
соответствует физически реализуемое преобразование матриц плотности 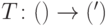 . Имеет смысл и упрощенная модель: по аналогии с множеством переходов
. Имеет смысл и упрощенная модель: по аналогии с множеством переходов 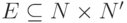 определим пространство ошибок — произвольное линейное пространство
определим пространство ошибок — произвольное линейное пространство 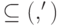 . (Таким образом, квантовая ошибка — это любой линейный оператор
. (Таким образом, квантовая ошибка — это любой линейный оператор  ). Есть и прямой аналог множества
). Есть и прямой аналог множества 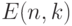 . Рассмотрим
. Рассмотрим  . Через
. Через ![\calE[A]](/sites/default/files/tex_cache/14bd103f8216f55b88243943d03a0d18.png) обозначим те ошибки, которые действуют на q-битах из множества
обозначим те ошибки, которые действуют на q-битах из множества  и не действуют на остальных q-битах, т.е.
и не действуют на остальных q-битах, т.е. ![\calE[A]=\LL(\BB^{\otimes A})\otimes I_{\BB^{\otimes[n]\setminus A}}](/sites/default/files/tex_cache/1bcd91df1d759f09ef71fab5c95187cb.png) (здесь и далее
(здесь и далее ![[n]](/sites/default/files/tex_cache/de504dafb2a07922de5e25813d0aaafd.png) обозначает множество всех q-битов
обозначает множество всех q-битов 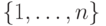 ). Тогда полагаем
). Тогда полагаем
![\calE(n,k)=\sum_{|A|\le k}^{} \calE[A].](/sites/default/files/tex_cache/f7dab48d75d81903852ced3f8f81e36f.png)
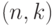 .
.Но перед тем, как заняться изучением кодов, устойчивых к ошибкам из 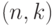 , рассмотрим аналог модели независимо распределенных ошибок в квантовом случае и его связь с ошибками из
, рассмотрим аналог модели независимо распределенных ошибок в квантовом случае и его связь с ошибками из 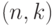 .
.

