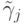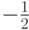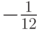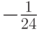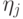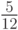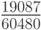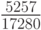Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений
8.3. Методы Адамса
Для решения ОДУ или систем ОДУ существуют одностадийные методы Адамса (линейные многошаговые методы), суть которых заключается в следующем.
Пусть известно приближенное решение в некоторых узлах расчетной сетки: tn, tn - 1, ..., tn - m. В окрестности этих узлов заменим f(t, x(t)) интерполяционным полиномом, записанным в форме Ньютона ([8.1], [8.2], а также "Интерполяция функций" ):
f(t) = f(tn) + f(tn, tn - 1) (t - tn) + + f(tn, tn - 1, tn - 2) (t - tn) (t - tn - 1) + + f(tn, tn - 1, tn - 2, tn - 3) (t - tn) (t - tn - 1) (t - tn - 2) + ...
Для того чтобы вычислить решение в точке n + 1, запишем его в интегральном виде
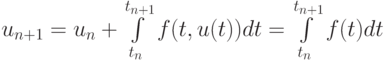
и подставим в него интерполяционный полином с переменным шагом
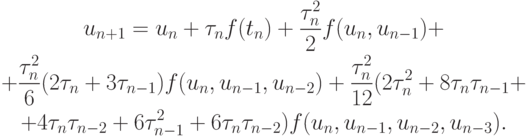
Здесь 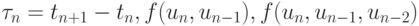 и т.д. - разделенные разности.
и т.д. - разделенные разности.
Эта формула четвертого порядка точности. Если опустить последнее слагаемое,
то получим формулу третьего порядка, если опустить еще и предпоследнее, то — второго, и т.д. Если же положить 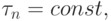 то формула значительно упростится:
то формула значительно упростится:
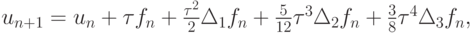
где  — k - я конечная разность.
— k - я конечная разность.
Для того чтобы начать вычисления по данному варианту метода Адамса, необходимо знать решение в четырех точках. Это можно сделать, например, с помощью методов Рунге - Кутты. Кроме того, коэффициент при погрешности, например, для метода четвертого порядка точности Рунге - Кутты существенно меньше соответствующего коэффициента для метода Адамса.
Первые четыре метода Адамса, от первого до четвертого порядка точности с постоянным шагом интегрирования, представляются в виде
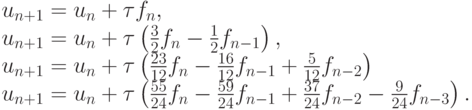 |
( 8.7) |
В общем виде методы Адамcа могут быть записаны следующим образом:
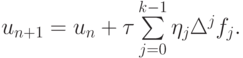
Значительно большее значение в вычислительной практике имеют неявные методы Адамса, которые можно записать как
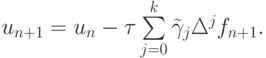
Первые четыре неявных метода имеют вид
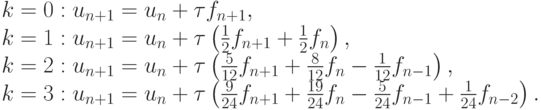
Первая и вторая формулы — неявный метод Эйлера и неявный метод трапеций соответственно. Порядок аппроксимации приведенных методов — с первого по четвертый соответственно.
Для k = 8 коэффициент 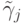 можно
представить в виде таблицы (табл. 8.19) и ввести следующие обозначения:
можно
представить в виде таблицы (табл. 8.19) и ввести следующие обозначения: 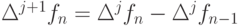 — "разности назад",
— "разности назад", 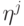 — коэффициенты, которые можно представить в виде таблицы (для k = 8 табл. 8.2). Для k = 1 получается уже знакомый явный метод Эйлера.
— коэффициенты, которые можно представить в виде таблицы (для k = 8 табл. 8.2). Для k = 1 получается уже знакомый явный метод Эйлера.