Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений
Таким образом, можно написать приближенное равенство:
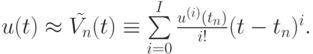
Полагая
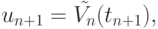
получаем приближенное значение u(t) в точке t = tn +
1. При I = 1 и  получаем метод Эйлера:
получаем метод Эйлера:
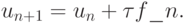
Этот способ не получил распространения в практике решения дифференциальных
уравнений из - за необходимости вычисления производных u(i), где  По затратам машинного времени он заметно уступает другим методам, о которых будет идти речь далее.
По затратам машинного времени он заметно уступает другим методам, о которых будет идти речь далее.
В настоящее время в практике решения жестких систем ОДУ применяют так называемые многозначные методы, основанные на разложении в ряд Тейлора и вычислении производных. О жестких системах ОДУ будет рассказано ниже.
Рассмотрим еще один способ получения простейших одношаговых расчетных схем для численного решения уравнения (8.1), для чего напишем равенство
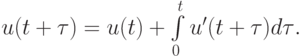
После аппроксимации интеграла в правой части по формуле прямоугольников и замене его на величину 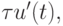 получим
получим

или

поскольку u'(t) = f(t, u).
Опуская член 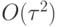 и обозначая
и обозначая 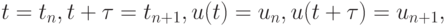 получим метод Эйлера.
получим метод Эйлера.
Если рассматриваемый интеграл заменить формулой трапеций, получим
![$ u(t + {\tau}) = u(t) + \frac{{\tau}}{2} [u^{\prime}(t) + u^{\prime}(t + {\tau})] + O({\tau}^3 ), $](/sites/default/files/tex_cache/1b9de25cc9b98c660dcd21ebe854e983.png)
откуда имеем
![$ u_{n + 1} = u_n + \frac{{\tau}}{2} [f(t_n, u_n) + f(t_{n + 1}, u_{n + 1})]. $](/sites/default/files/tex_cache/b455be5445600dd7bf595c65594bd5fd.png)
Этот метод называется неявным методом трапеций. Для того чтобы метод был явным, его делают двухэтапным:
![\begin{gather*}
\tilde u_{n + 1} = u_n + {\tau}f(f_n, u_n), \\
u_{n + 1} = u_n + \frac{{\tau}}{2}[f(t_n, u_n) + f(t_{n + 1}, \tilde u_{n + 1})],
\end{gather*}](/sites/default/files/tex_cache/d0ce6049832a6269e770e96e7145dcaf.png)
где 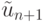 — вспомогательная величина,
вычисляемая на промежуточном этапе. Если этот же интеграл приблизить формулой прямоугольников со средней точкой, то получим
— вспомогательная величина,
вычисляемая на промежуточном этапе. Если этот же интеграл приблизить формулой прямоугольников со средней точкой, то получим
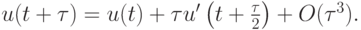
Снова воспользовавшись дифференциальным уравнением (8.1), преобразуем последнее выражение к виду
![$ u(t + {\tau}) = u(t) + {\tau}f\left[{t + \frac{{\tau}}{2},
u\left({t + \frac{{\tau}}{2}}\right)}\right] + O({\tau}^3 ). $](/sites/default/files/tex_cache/1fa5287e9171b95ce3728d5f37b0f31d.png)
Соответствующий неявный метод имеет вид
![$ u_{n + 1} = u_n + {\tau}f\left[{t_n + \frac{{\tau}}{2}, u\left({t_n + \frac{{\tau}}{2}}\right)}\right] ; $](/sites/default/files/tex_cache/fb46c9ef73ddc1b37f248fdeb767bc36.png)
для его явной реализации можно воспользоваться следующей двухэтапной формулой: