Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений
8.5. Устойчивость методов Рунге - Кутты
Для исследования устойчивости методов Рунге - Кутты для численного решения задачи

представим ее дискретный аналог в виде
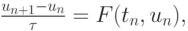 |
( 8.8) |
здесь F(t, x) — функция приращения метода Рунге - Кутты, которая, конечно, связана с функцией правой части системы ОДУ.
Теорема 2 ( Устойчивость методов Рунге - Кутты [8.3], [8.9]). Пусть f(t, x) Липшиц - непрерывна по второму аргументу, т.е.
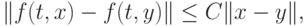
причем это условие выполняется для каждого t, 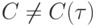 и
и 
Тогда разностное уравнение (8.8) устойчиво и имеет место оценка
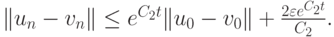 |
( 8.9) |
Здесь un, vn - решения близких систем разностных уравнений:
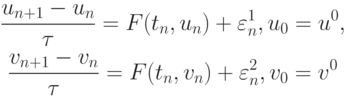
и 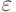 — максимальная погрешность при вычислении
правой части системы, т.е. для всех n (включая нуль)
— максимальная погрешность при вычислении
правой части системы, т.е. для всех n (включая нуль)
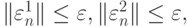
а постоянная C2 незначительно отличается от C.
Сформулируем вначале следующую лемму.
Лемма 1. Пусть C — постоянная Липшица для функции правых частей системы (8.1), тогда функция приращения F(t, u) для метода (8.8) удовлетворяет следующему неравенству:
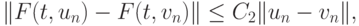
где
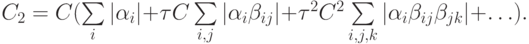
Суммирование в правой части последнего равенства ведется по каждому
индексу от 1 до r > — числа стадий метода. Число сумм в скобках, конечно, тоже равно r >. Отметим также, что если в таблице Бутчера все
коэффициенты неотрицательны (такой метод Рунге - Кутты, по аналогии с методом численного интегрирования, назовем правильным), то из условий порядка ( аппроксимации ) будет следовать, что в скобках стоят первые r > членов разложения 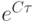 в ряд Тейлора. Отсюда необходимое требование (в формулировке теоремы) к малости
в ряд Тейлора. Отсюда необходимое требование (в формулировке теоремы) к малости 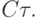 В случае наличия отрицательных коэффициентов в таблице Бутчера константа Липшица C2 увеличится незначительно — число стадий метода конечно и невелико (в настоящее время известны методы максимум с 17 стадиями, [8.6]).
В случае наличия отрицательных коэффициентов в таблице Бутчера константа Липшица C2 увеличится незначительно — число стадий метода конечно и невелико (в настоящее время известны методы максимум с 17 стадиями, [8.6]).
Доказательство данной леммы довольно простое, но громоздкое. Читатель может проделать это самостоятельно.
Доказательство теоремы.
Рассмотрим эти близкие уравнения. Вычитая из первого уравнения второе, получим
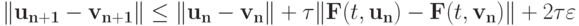 |
( 8.10) |
или, учитывая условие Липшица,
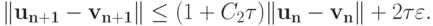
Здесь константа C2 — постоянная Липшица функции приращения метода Рунге - Кутты, выражение для нее приведено выше в формулировке леммы 8.1.
Далее, применяя последовательно это неравенство, получим оценки:
![\begin{gather*}
\|\mathbf{u_1} - \mathbf{v_1}\| \le (1 + C_2{\tau})\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon, \\
\|\mathbf{u_2} - \mathbf{v_2}\| \le (1 + C_2{\tau})\|\mathbf{u_1} - \mathbf{v_1}\| + 2{\tau}\varepsilon \le {(1 + C_2{\tau})}^2\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon[1 + (1 + C_2{\tau})], \\
\|\mathbf{u_3} - \mathbf{v_3}\| \le (1 + C_2{\tau})\|\mathbf{u_2} - \mathbf{v_2}\| + 2{\tau}\varepsilon \le \\
\le {(1 + C_2{\tau})}^3\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon[1 + (1 + C_2{\tau}) + {(1 + C_2{\tau})}^2], \\
\|\mathbf{u_n} - \mathbf{v_n}\| \le {(1 + C_2{\tau})}^{n}\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon[1 + (1 + C_2{\tau}) + \ldots + {(1 + C_2{\tau})}^{n - 1}],
\end{gather*}](/sites/default/files/tex_cache/c2e5c72d1d37a52633f6a54b2a5a152e.png)
откуда, после суммирования прогрессии, имеем
![\begin{gather*}
\|\mathbf{u_n} - \mathbf{v_n}\| \le {(1 + C_2{\tau})}^{n}\|\mathbf{u_0} - \mathbf{v_0}\| + 2{\tau}\varepsilon\frac{{(1 + C_2{\tau})}^{n} - 1}{(1 + C_2{\tau}) - 1} \le \\
\le {(1 + C_2{\tau})}^{n}[\|\mathbf{u_0} - \mathbf{v_0}\| + \frac{2\varepsilon}{C_2}].
\end{gather*}](/sites/default/files/tex_cache/72c7288a57d1ad3dbb6c52d31342be60.png)
Далее полагаем 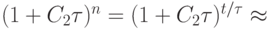
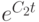 при
при 
После подстановки экспоненты в последнюю оценку получим неравенство (8.9).
Заметим, что экспоненциальный множитель в неравенстве (8.9) при больших t велик, а оценка, в наиболее общем случае, в предположении Липшиц - непрерывности функции  неулучшаема. Однако в некоторых важных частных случаях эту оценку можно улучшить, рассматривая более
тонкие свойства рассматриваемой функции. Докажем следующее утверждение [8.9], рассматривая задачу Коши для системы ОДУ.
неулучшаема. Однако в некоторых важных частных случаях эту оценку можно улучшить, рассматривая более
тонкие свойства рассматриваемой функции. Докажем следующее утверждение [8.9], рассматривая задачу Коши для системы ОДУ.
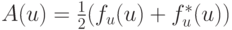
строго отрицательна, т.е.

для любых 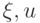 и a > 0 (траектория, в окрестности которой выполняется это условие, называется устойчивой ).
и a > 0 (траектория, в окрестности которой выполняется это условие, называется устойчивой ).
Тогда при интегрировании правильным методом Рунге - Кутты k - го порядка аппроксимации погрешность приближенного решения есть 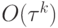 при любом t > 0 при выполнении условий
при любом t > 0 при выполнении условий 
Утверждение будет доказано, если в оценке устойчивости метода не будет содержаться множитель eCt.
