НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3909 / 1192 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Дается понятие жесткой системы (ЖС ОДУ). Рассматриваются неявные методы Рунге - Кутты и Гира для решения ЖС ОДУ. Исследуется устойчивость методов.

Ключевые слова: вектор, матрица, жесткие системы ОДУ, определение, затраты, ПО, спектр матрицы Якоби, отношение, константы, матрица Якоби, неявные и диагонально-неявные, устойчивость, модуль, функция, А-устойчивость, жесткая устойчивость, метод Эйлера, задача Коши, характеристическое уравнение, плоскость, поле, ветвь, численное интегрирование, интегрирование, алгоритм, системы нелинейных уравнений, алгебраические системы, разложение в ряд, значение, метод трапеций, метод прямоугольников, методы Рунге-Кутты, таблицы Бутчера, неявные и диагонально-неявные, методы Розенброка, класс, вычисление, связь, управляющие, коэффициенты, вывод, методы Гира, метод адамса, размерность, метод Гира, представление Нордсика, равенство, выражение, представление, биномиальные коэффициенты

9.1. Явление жесткости. Предварительные сведения

Рассмотрим в качестве примера две задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ) [9.1], [9.2]:

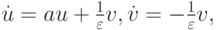
$\dot {u} = au + \frac{1}{\varepsilon } v, \dot {v} = - \frac{1}{\varepsilon } v,$

с начальными данными u(0) = u₀, v(0) = v₀ ; здесь 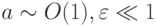$a \sim O(1), \varepsilon \ll 1$ ; и линейную систему с постоянными коэффициентами

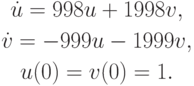
$\begin{gather*} \dot {u} = 998u + 1998v, \\ \dot {v} = - 999u - 1999v, \\ u(0) = v(0) = 1. \end{gather*}$

Решением первой задачи Коши являются функции

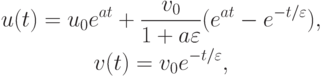
$\begin{gather*} u(t) = u_0 e^{at} + \frac{{v_0 }}{{1 + a\varepsilon }} (e^{at} - e^{- t/\varepsilon }), \\ v(t) = v_0 e^{- t/\varepsilon }, \end{gather*}$

а второй -

u(t) = 4e^{- t} - 3e^{- 1000t},
v(t) = - 2e^{- t} + 3e^{- 1000t}.

В обоих случаях решение состоит из двух экспонент: быстро убывающей и относительно медленно изменяющейся. Отметим, что абсолютные величины собственных значений матриц рассматриваемых линейных систем ОДУ при их представлении в виде

$\dot {u} = Au,$

( u — вектор - столбец, A — матрица с постоянными коэффициентами) существенно различаются. Так, в первом случае 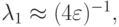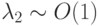$\lambda _{1} \approx (4\varepsilon )^{- 1},$ $\lambda _{2} \sim O(1)$ ; во втором: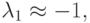 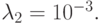$\lambda _{1} \approx - 1,$ $\lambda _{2} = 10^{- 3}.$ В обоих случаях имеем:

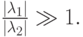
$\frac{{|\lambda_1 |}}{{|\lambda_2 |}} \gg 1.$

При моделировании физических процессов причина такой разницы в собственных числах заключена в существенно различных характерных временах процессов, описываемых системами ОДУ. Наиболее часто подобные системы встречаются при моделировании процессов в ядерных реакторах, при решении задач радиофизики, астрофизики, физики плазмы, биофизики, химической кинетики. Последние задачи часто могут быть записаны в виде [9.3]:

$\frac{d u_k}{d t} = \sum\limits_{i = 1}^{N}{\sum\limits_{j = 1}^{N}{a_{_{ij}}^{k} u_i u_j}, } k = 1 \div N;$

где u_k — концентрации веществ, участвующих в химических реакциях, скорости протекания которых характеризуются коэффициентами 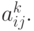$a_{ij}^{k}.$ В качестве примера приведем одну из систем химической кинетики, описывающую изменение концентрации трех веществ, участвующих в реакции для случая полного перемешивания [9.1].

Пример 1. Обозначим концентрации трех веществ, участвующих в реакции, через u₁, u₂ и u₃, тогда

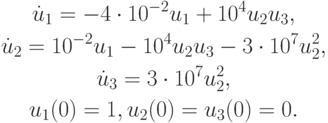
$\begin{gather*} \dot u_1 = - 4 \cdot 10^{- 2} u_1 + 10^4 u_2 u_3, \\ \dot u_2 = 10^{- 2} u_1 - 10^4 u_2 u_3 - 3 \cdot 10^7 u_2^2, \\ \dot u_3 = 3 \cdot 10^7 u_2^2, \\ u_1 (0) = 1, u_2 (0) = u_3 (0) = 0. \end{gather*}$

Участки решения, характеризующиеся быстрым и медленным его изменением, называются пограничным слоем и квазистационарным режимом, соответственно.

Трудности численного решения подобных систем ОДУ, получивших название жестких (определение жесткой системы приведено ниже), связаны с выбором шага интегрирования. Дело в том, что характерные времена исследуемых процессов могут различаться более чем в 10¹² раз. Следовательно, если при численном решении системы

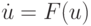
$\dot {u} = {F}(u)$

выбирать шаг из условия

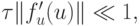
$\tau\|f^{\prime}_u (u)\|\ll 1,$

то он будет соответствовать самому быстрому процессу. В данном случае затраты машинного времени для исследования самых медленных процессов будут неоправданно велики. По этой причине имеются следующие альтернативы в выборе подхода к численному решению рассматриваемых задач.

Численно решать систему ОДУ с шагом
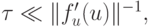
${\tau}\ll \|f^{\prime}_u (u)\|^{- 1},$

т.е. с учетом характерных времен всех процессов, описываемых данной системой.
Решать систему ОДУ с различными шагами, соответствующими физическим процессам с существенно различными характерными временами. В этом случае необходимо задавать условия перехода к другому шагу интегрирования.
"Пренебречь" быстропротекающими процессами и численно рассматривать лишь медленные, проводя интегрирование с шагом, превышающим характерные времена быстрых процессов. В этом случае придется конструировать численные методы, позволяющие проводить расчеты с шагом
${\tau}\gg \|f^{\prime}_u (u)\|^{- 1}.$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

9.1. Явление жесткости. Предварительные сведения

Вопросы и ответы