НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

Жесткий спектр:
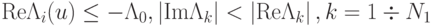
${\mathop{\mathrm{Re}}\nolimits}\Lambda_i (u) \le - \Lambda_0, \left|{\mathop{\mathrm{Im}}\nolimits}\Lambda_k\right| < \left|{\mathop{\mathrm{Re}}\nolimits}\Lambda_k\right|, k = 1 \div N_1$

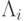( $\Lambda _{i}$ — собственные значения матрицы Якоби ); $\Lambda _{0} > 0$
Мягкий спектр:
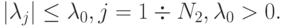
$|{\lambda_j}| \le \lambda_0, j = 1 \div N_2, \lambda_0 > 0.$

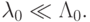
При этом $\lambda_0 \ll \Lambda_0 .$

Отношение 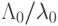$\Lambda _{0}/\lambda _{0}$ называется показателем жесткости системы. В дальнейшем будем полагать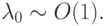 $\lambda _{0} \sim O(1).$

Проблему численного решения жестких систем ОДУ рассмотрим на примере модельной линейной системы вида:

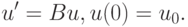( 9.1)

Ее точное решение задается формулой

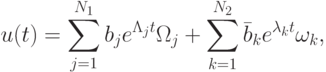${{u}(t) = \sum\limits_{j = 1}^{N_1}{b_j e^{\Lambda_j t}{\Omega }_j} + \sum\limits_{k = 1}^{N_2 }{\bar {b}_k e^{\lambda_k t}{\omega }_k}, }$

( 9.2)

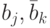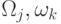где константы интегрирования $b_j, \bar b_k$ соответствуют жесткой и мягкой частям спектра ; $\Omega _{j}, \omega _{k}$ — собственные векторы матрицы Якоби, соответствующие собственным значениям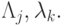 $\Lambda _{j}, \lambda _{k}.$

В этом решении видны две части: первая (жесткая) убывает как 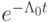$e^{- \Lambda_0 t}$ на временном интервале $[t_0, O(\Lambda_0^{- 1})]$ (пограничный слой), вторая заметно изменяется на интервале $[t_0, O(\Lambda_0^{- 1})]$ (квазистационарный режим).

Если провести аппроксимацию линейной системы ОДУ с помощью явного метода Эйлера

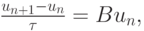
$\frac{u_{n + 1} - u_n}{{\tau}} = Bu_n,$

или

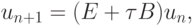
$u_{n + 1} = (E + \tau B)u_{n},$

то общее решение такой системы разностных уравнений будет иметь вид

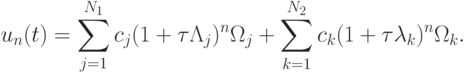$u_n (t) = \sum\limits_{j = 1}^{N_1}{c_j(1 + {\tau}\Lambda_j)^n \Omega_j} + \sum\limits_{k = 1}^{N_2 }{c_k (1 + {\tau}\lambda_k)^{n}{\Omega_k}.$

( 9.3)

Второе слагаемое в этом решении аппроксимирует второе слагаемое в точном решении (9.2), а первое быстро растет и приводит к абсурдному результату.

Теперь проведем аппроксимацию линейной системы ОДУ (9.1) с помощью неявного метода Эйлера:

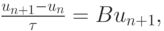
$\frac{u_{n + 1} - u_n}{{\tau}} = Bu_{n + 1},$

или

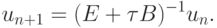
$u_{n + 1} = (E + \tau B)^{ - 1}u_{n}.$

Общее решение такого разностного уравнения имеет следующий вид:

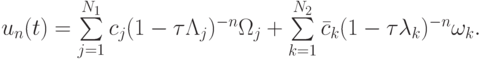
$u_n (t) = \sum\limits_{j = 1}^{N_1 }{c_j (1 - {\tau}\Lambda_j)^{- n}{\Omega }_j} + \sum\limits_{k = 1}^{N_2 }{\bar c_k (1 - {\tau}\lambda_k)^{- n}{\omega }_k}.$

В этом случае второе слагаемое ведет себя так же, как и точное решение, а первое стремится к нулю как 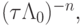$(\tau \Lambda _{0})^{- n},$ т.е. его поведение качественно совпадает с точным в области пограничного слоя.

В практике численных исследований жестких задач часто не нужно изучать поведение решения в пограничном слое, и можно воспользоваться неявными методами. Но в случае необходимости исследовать этот слой можно с шагом ${\tau} \ll \Lambda_0^{- 1}.$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

Вопросы и ответы