Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений
- Сингулярно - возмущенная система — модель двухлампового
генератора Фрюгауфа.
Система более высокой размерности, имеющая решение в виде релаксационного цикла, приведена в [9.18] (см. также [9.21]). Она имеет вид:
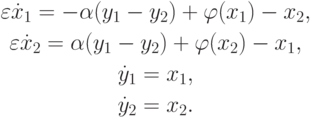
Здесь
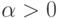 — константа порядка единицы, функция
— константа порядка единицы, функция  x1(0) = x2(0) = 0, y1 = 2, y2 = 0, Tk = 20,
x1(0) = x2(0) = 0, y1 = 2, y2 = 0, Tk = 20, 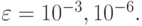
- Простейшая модель гликолиза
Простейшая модель гликолиза описывается уравнениями следующего вида [9.21]:
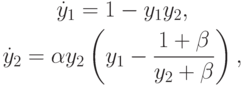
предложенными Дж. Хиггинсом. В системе
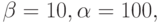 200, 400, 1000. Начальные условия
для системы: y1(0) = 1, y2(0) = 0, 001, Tk = 50. Решение этой системы — релаксационные автоколебания (жесткий предельный цикл).
200, 400, 1000. Начальные условия
для системы: y1(0) = 1, y2(0) = 0, 001, Tk = 50. Решение этой системы — релаксационные автоколебания (жесткий предельный цикл). - Пример жесткой системы — модель химических реакций Робертсона
Один из первых и самых популярных примеров жесткой системы ОДУ принадлежит Робертсону (1966) и имеет вид, типичный для моделей химической кинетики — в правой части системы стоят полиномы второй степени от концентраций (сравните с орегонатором).
Система Робертсона имеет вид [9.9]
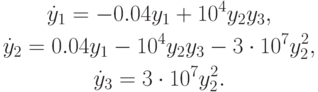
Начальные условия для системы таковы: y1(0) = 1, y2(0) = 0, y3(0) = 0. Рассматриваются следующие величины отрезка интегрирования: Tk = 40 (в работе Робертсона рассматривался именно такой отрезок интегрирования), Tk = 100, 1000, ..., 1011. О свойствах задачи см. в [9.9].
-
Модель дифференциации растительной ткани
Данный пример из [9.9] — типичный случай биохимической модели "умеренной" размерности (современные модели, например, фотосинтеза включают сотни уравнений подобного типа). Хотя данная модель является умеренно жесткой, тем не менее, ее лучше решать с помощью методов, предназначенных для решения ЖС ОДУ.
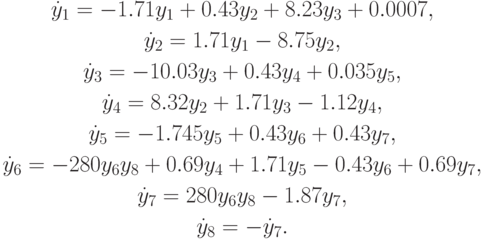
Начальные значения всех переменных системы равны 0, кроме y1(0) = 1 и y8(0) = 0.0057. Длина отрезка интегрирования Tk = 421, 8122.
-
Задача E5
Еще одна модель химической реакции из [9.9], получившая свое название Е5 в более ранних публикациях.
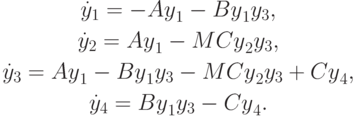
Начальные условия:
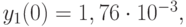 а все остальные
переменные равны 0. Значения коэффициентов модели следующие:
а все остальные
переменные равны 0. Значения коэффициентов модели следующие: 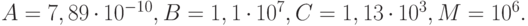 Первоначально задача ставилась на отрезке Tk = 1000, но впоследствии было обнаружено, что она обладает нетривиальными свойствами вплоть до времени Tk = 1013 (подробнее см. [9.9]).
Первоначально задача ставилась на отрезке Tk = 1000, но впоследствии было обнаружено, что она обладает нетривиальными свойствами вплоть до времени Tk = 1013 (подробнее см. [9.9]).Обратить особое внимание, что в процессе расчетов приходится иметь дело с очень малыми концентрациями реагентов (малы значения y2, y3 и y4 ). Как "подправить" постановку задачи E5?
-
Уравнение Релея
Уравнение Релея во многом похоже на уравнение Ван - дер - Поля [9.21]. Рассматривается задача вида
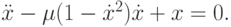
Решить задачу, записав уравнение Релея в виде системы ОДУ. Начальные условия:

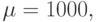 Tk = 1000.
Tk = 1000. -
Экогенетическая модель
Рассмотрим пример системы уравнений, которая описывает изменения численности популяций двух видов и эволюцию некого генетического признака
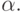 Система ОДУ имеет вид
Система ОДУ имеет вид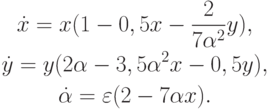
Параметры задачи таковы:
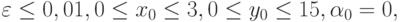 Tk = 1500. Наличие малого параметра в третьем уравнении системы показывает, что генетический признак меняется медленнее, чем численность популяций. Решение системы — релаксационные колебания.
Tk = 1500. Наличие малого параметра в третьем уравнении системы показывает, что генетический признак меняется медленнее, чем численность популяций. Решение системы — релаксационные колебания.Задача описана в статье [9.22].
-
Экогенетическая модель
Еще один пример жесткой системы описан в статье [9.22]. Более интересный случай — численность двух популяций зависит от взаимодействия между ними и двух медленно меняющихся генетических признаков.
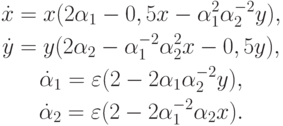
Параметры задачи таковы:
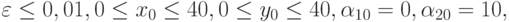 Tk = 2000.
Tk = 2000.Рассмотреть также модификацию предыдущей системы [9.22]:
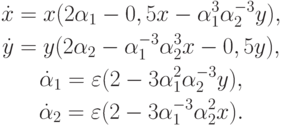
Параметры задачи:
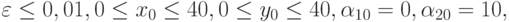 Tk = 2000.
Tk = 2000.
