НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 7: Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3992 / 1259 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Рассматривается задача алгебраической интерполяции. Обусловленность задачи исследуется на основе рассмотрения константы Лебега. Доказывается теорема об остаточном члене интерполяции. Выводятся формулы алгебраической интерполяции с кратными узлами. Рассматривается задача гладкого восполнения функции (локальными и нелокальными сплайнами, а также естественный базис в пространстве сплайн - функций — B - сплайны.

Ключевые слова: интерполяция, расстояние, ПО, функция, кусочно-линейная интерполяция, равенство, разность, метод конечных элементов, сплайны, обобщенный полином, определитель матрицы, матрица, определитель, вектор, базисные функции, полином, интерполяционный полином в формах Лагранжа и Ньютона, выражение, место, разделенные разности, симметричная функция, численное дифференцирование, метод неопределенных коэффициентов, минимакс, старший коэффициент, Произведение, постоянная Лебега, объект, устойчивость, оператор проекции, пространство, норма, погрешность, кратность, значение, многочлен, производные, доказательство, вторая производная, константы, метод решения, минимум, коэффициенты, B-сплайны, bell, моделирование, В - сплайны, функциональное пространство, прямой, координаты, длина

6.1. Постановка задачи интерполяции

Пусть задана совокупность узлов интерполяции или сетка на некотором отрезке [a, b]. В простейшем случае сетка — равномерная, т.е. расстояние между соседними узлами одинаково. В дальнейшем также рассмотрим неравномерные сетки.

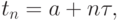
Совокупность узлов $\left\{{t_n}\right\}_{n = 0}^N,$ $t_{n} = a + n\tau,$ $\tau = (b - a)/N,$ $t \in \left[{a, b}\right].$
Сеточная проекция функции f(t) на [a, b], т.е. таблица 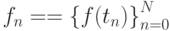$f_n = = \left\{{f(t_n)}\right\}_{n = 0}^N$ ; эту таблицу задает оператор ограничения на сетку или рестрикции (от английского restriction )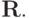 $\mathbf{R}.$

Задача состоит в том, чтобы по таблице {f_n} восстановить непрерывную функцию. Обозначим ее через F(t). Разумеется, она отличается от исходной функции f(t), причем такое восстановление неоднозначно и осуществляется оператором интерполяции 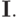$\mathbf{I}.$ Сама функция F(t) называется интерполирующей или интерполянтом. Необходимо оценить потерю информации при действии этого оператора, т. е. величину |f(t) - F(t)|, зависящую от типа оператора интерполяции и свойств f(t), в частности, ее гладкости. Таким образом, имеем схему:

$f(t) \mathop \to\limits_{\mathbf{R}} \left\{{f_n}\right\}_{n = 0}^{N} \mathop \to\limits_{\mathbf{I}} F(t).$

6.2. Кусочно - линейная интерполяция

Простейший способ интерполяции — кусочно - линейная, требующая минимальных требований на гладкость функции f(t). При таком способе интерполяции соседние точки ( t_n, f_n ) и ( t_{n + 1}, f_{n + 1} ) соединяют отрезками прямых

$F(t) = \frac{f_{n + 1} (t - t_n) + f_n (t_{n + 1} - t)}{t_{n + 1} - t_n}, t \in [t_n , t_{n + 1} ].$

Теорема. Пусть f(t) — Липшиц непрерывная функция, т.е. 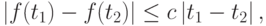$| f(t_1 ) - f(t_2 ) | \le c \left|{t_1 - t_2 }\right|,$ тогда

$$ \left|{f(t) - F(t)}\right| \le c\frac{\tau }{2} $.$

Примечание. Если сетка неравномерная и 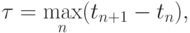$\tau = \max\limits_n (t_{n + 1} - t_n),$ то теорема верна и для этого случая.

Доказательство.

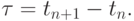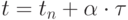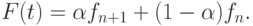
Пусть $t \in [t_n , t_{n + 1} ],$ обозначим $\tau = t_{n + 1} - t_{n}.$ Тогда $t = t_n + \alpha \cdot \tau$ ; $0 \le \alpha \le 1.$ В силу линейности f(t) имеем равенство $F(t) = \alpha f_{n + 1} + (1 - \alpha )f_n.$

Оценим разность

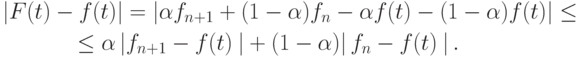
$\begin{gather*} \left|{F(t) - f(t)}\right| = \left|{\alpha f_{n + 1} + (1 - \alpha )f_n - \alpha f(t) - (1 - \alpha )f(t)}\right| \le \\ \le \alpha \left|{f_{n + 1} - f(t)\left. {}\right| + (1 - \alpha )}\right|f_n - f(t)\left. {}\right|. \end{gather*}$

Поскольку 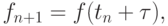$f_{n + 1} = f(t_{n} + \tau ),$ имеем

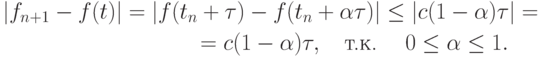
$\begin{multline*} \left|f_{n + 1} - f(t)\right| = \left|f(t_n + \tau) - f(t_n + \alpha\tau)\right| \le \left|c(1 - \alpha )\tau\right| = \\ = c(1 - \alpha)\tau, \quad \mbox{т.к. }\quad 0 \le \alpha \le 1. \end{multline*}$

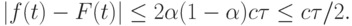
Аналогично $\left|{f_n - f(t)}\right| \le c\alpha \tau.$ В таком случае $\left|{f(t) - F(t)}\right| \le 2\alpha (1 - \alpha ) c\tau \le c\tau/2.$

Замечание. Простой аппарат кусочно - линейной интерполяции позволяет ввести объекты, на которых базируется один из наиболее известных современных численных методов — метод конечных элементов. Сетке { t_n } ставится в соответствие набор базисных функций 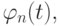$\varphi_n(t),$ каждая из которых сопоставляется своему узлу t_n, причем 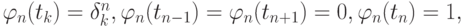$\varphi_n (t_k ) = \delta_k^{n}, \varphi_n (t_{n - 1}) = \varphi_n (t_{n + 1}) = 0, \varphi_n (t_n) = 1,$ а в остальных точках она вычисляется с помощью кусочно - линейной интерполяции.

Функция f(t) в этом случае представляется в виде

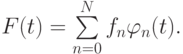
$F(t) = \sum\limits_{n = 0}^{N}{f_n}\varphi_n (t).$

В вычислительной математике часто используется кусочно - полиномиальная интерполяция. Так, эрмитовым кубическим интерполянтом называется кусочно - кубический интерполянт с непрерывной производной, кубическим сплайном называется кусочно - кубический интерполянт с двумя непрерывными производными. О сплайнах речь пойдет ниже.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Интерполяция функций

6.1. Постановка задачи интерполяции

6.2. Кусочно - линейная интерполяция

Вопросы и ответы