Интерполяция функций
6.7. Многочлены Чебышёва и минимизация остаточного члена интерполяции
Многочленом Чебышева первого рода называется функция Tn(t) = cos (n arccos t), где ![t \in \left[{- 1, 1}\right], n = 0, 1, \ldots](/sites/default/files/tex_cache/5829d985ecffd7a21962de2d00a36b05.png)
Убедимся в том, что функция Tn(t) действительно является многочленом. При n = 0 и n = 1 имеем T0(t) = 1, T1(t) = t.
Положив 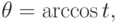 получим
получим 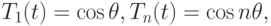
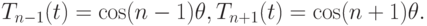 По формуле суммы косинусов
По формуле суммы косинусов  и справедливо рекуррентное соотношение Tn + 1(t) + Tn - 1(t) = 2T1(t)Tn(t), или Tn + 1(t) = 2t Tn(t) - Tn - 1(t). Отсюда следует вид записи полиномов Чебышева: T2 = 2t2 - 1, T3(t) = 4t3 - 3t, T4(t) = 8t4 - 8t2 + 1 и так далее. Функции Tn(t) являются многочленами степени n со
старшим членом 2n - 1tn.
и справедливо рекуррентное соотношение Tn + 1(t) + Tn - 1(t) = 2T1(t)Tn(t), или Tn + 1(t) = 2t Tn(t) - Tn - 1(t). Отсюда следует вид записи полиномов Чебышева: T2 = 2t2 - 1, T3(t) = 4t3 - 3t, T4(t) = 8t4 - 8t2 + 1 и так далее. Функции Tn(t) являются многочленами степени n со
старшим членом 2n - 1tn.
Введем также нормированные многочлены Чебышева

Нули многочлена Чебышева находятся из очевидного уравнения Tn(t) = cos (n arccos t) = 0, откуда
![$ t_m = \cos \left({\frac{{2m - 1}}{n}\pi }\right), m = 1, 2, \ldots n, t \in [{- 1, 1}] $.](/sites/default/files/tex_cache/0d3303ddf1be14ae993c517a4d060790.png)

![t \in [- 1, 1]](/sites/default/files/tex_cache/0b0d31b01b7633c74ee5be5966726b04.png) точки экстремумов есть
точки экстремумов есть 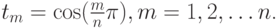
Нас интересует решение следующей задачи на минимакс: найти
![\min\limits_{\left\{t_n\right\}_{n = 0}^{N}}\left\{\max\limits_{t \in [- 1, 1] } \left|{\mathop \Pi\limits_{n = 0 }^{N}(t - t_n)}\right| \right\}](/sites/default/files/tex_cache/e8c79d3b51e50f666e568c6a855550a1.png)
чтобы путем выбора узлов сетки минимизировать остаточный член интерполяции. Эта задача была решена П.Л.Чебышевым.
Теорема. (Чебышева (без доказательства)) Среди всех многочленов степени  со старшим коэффициентом an равным единице, наименьшее уклонение от нуля, равное 21 - n, имеет нормированный полином Чебышева
со старшим коэффициентом an равным единице, наименьшее уклонение от нуля, равное 21 - n, имеет нормированный полином Чебышева ![\bar {T_n} (t) = 2^{1 - n} T_n (t), t \in \left[{- 1, 1}\right].](/sites/default/files/tex_cache/0f562e3435b4ecdfa02b875ab93dda29.png)
Это свойство полиномов Чебышева, наименьшее уклонение от нуля, можно
сформулировать по - другому: для любого полинома Pn(t) = tn + an - 1tn - 1 + ... + a0, отличного от 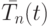 справедливо
справедливо ![2^{1 - n} = \max\limits_{\left[{- 1, 1}\right]} \left|{\bar {T_n} (t)}\right| < \max\limits_{\left[{- 1, 1}\right]} \left|{P_n (t)}\right|, t \in \left[{- 1, 1}\right].](/sites/default/files/tex_cache/3ed844865a1223ef1809b4af2c0a8793.png)
Если в качестве интерполяционных узлов выбрать нули полинома Чебышева, то
произведение 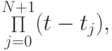 а также Rn(t) будут наименее уклоняющимися от нуля.
а также Rn(t) будут наименее уклоняющимися от нуля.
6.8. Обусловленность задачи интерполяции. Постоянная Лебега
В процессе вычислений значения интерполируемой функции известны с некоторой погрешностью. При работе на вычислительной машине ошибки округления неизбежны. Возникает вопрос о чувствительности интерполяционного полинома к ошибкам начальных данных (обусловленности задачи интерполяции ) и к ошибкам округления (вопрос вычислительной устойчивости). Интерполяционный полином — оператор, линейный по отношению к значениям интерполируемой функции. С учетом погрешности начальных данных полином в форме Лагранжа может быть записан следующим образом:
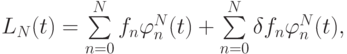
причем слагаемое

характеризует чувствительность к ошибкам начальных данных и ошибкам вычислений. Нас интересует оценка
![\max\limits_{t \in \left[{a, b}\right]} \left|{\Delta_N (t, \delta f)}\right| \le l_N \delta ;
\delta = \max\limits_{t \in \left[{a, b}\right]} \left|{\delta f_n}\right|, l_N = \max\limits_{t \in
[a, b]}\sum\limits_{n = 0}^{N} \left|\varphi_n^{N} (t)\right|,](/sites/default/files/tex_cache/72905e52e4805f8a55941b2cd7d023b2.png)
коэффициент lN называется постоянной Лебега.
Введем в рассмотрение еще один объект. Пусть 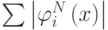 - сумма модулей всех базисных функций. Обозначим ее
- сумма модулей всех базисных функций. Обозначим ее 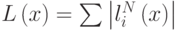 - функция Лебега (сетки). Тогда константа Лебега
- функция Лебега (сетки). Тогда константа Лебега ![l_N = \sup\limits_{x \in \left[{a, b}\right]}{L}\left(x\right).](/sites/default/files/tex_cache/f248297e4ccefc6acaf271165993e39c.png)
Так как функция Лебега зависит лишь от расположения узлов сетки, то и константа Лебега зависит лишь от введенной сетки. Обусловленность и устойчивость задачи интерполяции зависят от константы Лебега.
Если рассматривать оператор интерполяции как оператор проекции (проектор), переводящий элемент одного пространства (пространства сеточных функций) в другое (пространство непрерывно дифференцируемых функций), то постоянная Лебега есть норма такого оператора проекции. Подробнее об этом в [6.7].
Конечно, реальная погрешность при интерполяции будет заведомо меньше, чем приведенная выше оценка. Тем не менее, оценка является достижимой (это свойство нормы оператора). Наихудшим распределением погрешности будет такое распределение, когда погрешности максимальны и меняют знак от точки к точке. То, что при этом будет достижима приведенная выше оценка, следует из вида функции Лебега и каждой из базисных функций. Предлагаем читателям соответствующие построения провести самостоятельно.
Приведем (без доказательства) примерные оценки роста постоянной Лебега в зависимости от числа узлов сетки. Константа Лебега растет примерно как 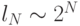 для равномерной сетки и
для равномерной сетки и 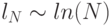 для сетки с чебышевским набором узлов. Доказано, что рост константы Лебега для последней сетки асимптотически стремится к минимально возможному, и сетка с чебышевскими узлами близка к оптимальной для задач интерполяции.
для сетки с чебышевским набором узлов. Доказано, что рост константы Лебега для последней сетки асимптотически стремится к минимально возможному, и сетка с чебышевскими узлами близка к оптимальной для задач интерполяции.
